题目内容
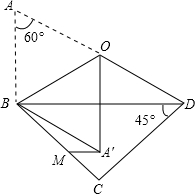 (2012•葫芦岛二模)如图,一副三角纸板拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为
(2012•葫芦岛二模)如图,一副三角纸板拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为| 6 |
| 2 |
| 6 |
| 2 |
分析:根据折叠的性质知AB=A′B=4;而O是Rt△ABD斜边AD的中点,则有AO=OB,由此可证得△ABO是等边三角形,那么∠A′BO=∠ABO=60°,进而可求出∠A′BM=15°;当A′M最小时,A′M⊥BC,此时△A′BM是直角三角形,取A′B的中点N,连接MN,那么∠A′NM=30°,A′N=MN=
A′B=
×4=2;过M作A′B的垂线,设垂足为H,在Rt△MNH中,根据∠A′NM的度数即可表示出NH,MH的长,进而可求出A′H的长,即可在Rt△A′MH中,根据勾股定理求出A′M的长.
| 1 |
| 2 |
| 1 |
| 2 |
解答: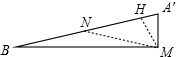 解:由折叠的性质知:AB=A′B=4,∠ABO=∠A′BO;
解:由折叠的性质知:AB=A′B=4,∠ABO=∠A′BO;
∵O是Rt△ABD斜边AD的中点,
∴OA=OB,即△ABO是等边三角形;
∴∠ABO=∠A′BO=60°;
∵∠ABD=90°,∠CBD=45°,
∴∠ABC=∠ABD+∠CBD=135°,
∴∠A′BM=135°-120°=15°;易知当A′M⊥BC时,A′M最短;
过M作MH⊥A′B于H,取A′B的中点N,连接MN,如图;
在Rt△A′BM中,N是斜边A′B的中点,则BN=NM=A′N=
×4=2,∠B=∠NMB=15°;
∴∠A′NM=30°;
∴MH=
MN=1,
∴NH=
=
;
∴A′H=A′N-NH=2-
;
由勾股定理得:A′M=
=
=
-
.
故答案为:
-
.
 解:由折叠的性质知:AB=A′B=4,∠ABO=∠A′BO;
解:由折叠的性质知:AB=A′B=4,∠ABO=∠A′BO;∵O是Rt△ABD斜边AD的中点,
∴OA=OB,即△ABO是等边三角形;
∴∠ABO=∠A′BO=60°;
∵∠ABD=90°,∠CBD=45°,
∴∠ABC=∠ABD+∠CBD=135°,
∴∠A′BM=135°-120°=15°;易知当A′M⊥BC时,A′M最短;
过M作MH⊥A′B于H,取A′B的中点N,连接MN,如图;
在Rt△A′BM中,N是斜边A′B的中点,则BN=NM=A′N=
| 1 |
| 2 |
∴∠A′NM=30°;
∴MH=
| 1 |
| 2 |
∴NH=
| MN2-NH2 |
| 3 |
∴A′H=A′N-NH=2-
| 3 |
由勾股定理得:A′M=
| A′H2+HM2 |
(
|
| 6 |
| 2 |
故答案为:
| 6 |
| 2 |
点评:此题主要考查了折叠的性质、直角三角形的性质以及勾股定理的应用,能够正确的构建出含特殊角的直角三角形是解答此题的关键.

练习册系列答案
相关题目


 (2012•葫芦岛二模)如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x 轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:
(2012•葫芦岛二模)如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x 轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系: