题目内容
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,经过点
,经过点![]() .
.
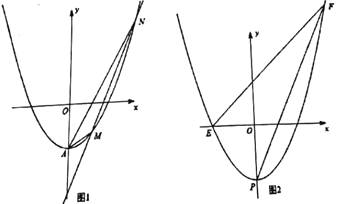
(1)求抛物线![]() 的解析式;
的解析式;
(2)如图1,直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() 的值;
的值;
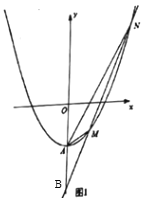
(3)如图2,将抛物线![]() 向下平移
向下平移![]() 个单位长度得到抛物线
个单位长度得到抛物线![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,交
,交![]() 轴的负半轴于点
轴的负半轴于点![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.
上.
①求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
②若![]() ,求
,求![]() ,
,![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①点
;(3)①点![]() 的坐标为
的坐标为![]() ;②
;②![]() .
.
【解析】
(1)根据顶点坐标设解析式为y=ax2-2,把B点坐标代入可求出a的值,即可得答案;(2)设直线![]() 交
交![]() 轴点
轴点![]() ,可得B的坐标为(0,4),可得AB的长,根据
,可得B的坐标为(0,4),可得AB的长,根据![]() 可得
可得![]() ,联立二次函数和一次函数的解析式可得
,联立二次函数和一次函数的解析式可得![]() ,根据一元二次方程根与系数的关系可得
,根据一元二次方程根与系数的关系可得![]() ,
,![]() ,进而可得答案;(3)①根据平移的性质可得抛物线C1的解析式,根据当F在抛物线C1上,可得
,进而可得答案;(3)①根据平移的性质可得抛物线C1的解析式,根据当F在抛物线C1上,可得![]() ,可得点P的坐标,令y=0,即可求出E点坐标;②作
,可得点P的坐标,令y=0,即可求出E点坐标;②作![]() 轴于点
轴于点![]() ,根据E、F坐标可得EH=FH,可得
,根据E、F坐标可得EH=FH,可得![]() ,根据∠FEO=2∠EFP及平行线的性质可得∠FPO=∠EFP =22.5°,设
,根据∠FEO=2∠EFP及平行线的性质可得∠FPO=∠EFP =22.5°,设![]() 交
交![]() 轴于点
轴于点![]() ,可得PD=DF=
,可得PD=DF=![]() OH,根据等腰直角三角形的性质可用a表示出PD的长,OH=a,列方程求出可得a的值,把a代入
OH,根据等腰直角三角形的性质可用a表示出PD的长,OH=a,列方程求出可得a的值,把a代入![]() 即可求出m的值.
即可求出m的值.
(1)已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
∴设抛物线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得:6=16a-2,
代入得:6=16a-2,
解得:![]() ,
,
∴抛物线![]() 的解析式为
的解析式为![]() .
.
(2)设直线![]() 交
交![]() 轴点
轴点![]() ,则点
,则点![]() 的坐标
的坐标![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
由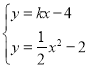 得
得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(3)①依题意得抛物线![]() 的解析式为
的解析式为![]() .
.
点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
∴顶点![]() 的坐标为
的坐标为![]() ,
,
令![]() ,即
,即![]() .
.
∴![]() ,
,![]() (舍去),
(舍去),
∴点![]() 的坐标为
的坐标为![]() .
.
②作![]() 轴于点
轴于点![]() ,
,
∵E(2-a,0),F(a,2a-2),
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∵FH//y轴,
∴∠FPO=∠PFH=22.5°,
∴∠FPO=∠EFP,
∴PD=FD,
设![]() 交
交![]() 轴于点
轴于点![]() ,过D作DG⊥FH于G,则DG=OH,
,过D作DG⊥FH于G,则DG=OH,
∵∠EFH=45°,
∴![]() ,
,
∵∠FEH=45°,a>2,
∴OD=OE=a-2,
∴PD=a-2-![]() =
=![]() ,
,
∵HO=a,
∴![]() ,
,
∴![]() ,
,![]() (舍去),
(舍去),
∴![]() .
.

 名师指导一卷通系列答案
名师指导一卷通系列答案