题目内容
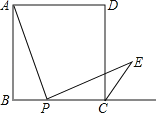
【题目】如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B,C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E,设BP=x,△PCE面积为y,则y与x的函数关系式是_____.
【答案】![]() .
.
【解析】
过E作EH⊥BC于H,证明△BAP∽△HPE,求出EH=x,所以y=![]() CPEH=
CPEH=![]() (4-x)x=-
(4-x)x=-![]() x2+2x,
x2+2x,
过E作EH⊥BC于H,
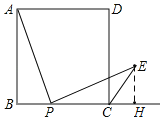
∵四边形ABCD是正方形,
∴∠DCH=90°,
∵CE平分∠DCH,
∴∠ECH=![]() ∠DCH=45°,
∠DCH=45°,
∵∠EHC=90°,
∴∠ECH=∠CEH=45°,
∴EH=CH,
∵四边形ABCD是正方形,AP⊥EP,
∴∠B=∠H=∠APE=90°,
∴∠BAP+∠APB=90°,∠APB+∠EPH=90°,
∴∠BAP=∠EPH,
∵∠B=∠EHP=90°,
∴△BAP∽△HPE,
∴![]() ,
,
即![]() ,
,
∴EH=x,
∴y=![]() CPEH=
CPEH=![]() (4﹣x)x=﹣
(4﹣x)x=﹣![]() x2+2x,
x2+2x,
故答案为:y=﹣![]() x2+2x.
x2+2x.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目