题目内容
【题目】图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.
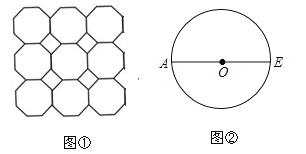
(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);
(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于 .
【答案】(1)作图见试题解析;(2)![]() .
.
【解析】
试题分析:(1)作AE的垂直平分线交⊙O于C,G,作∠AOG,∠EOG的角平分线,分别交⊙O于H,F,反向延长 FO,HO,分别交⊙O于D,B顺次连接A,B,C,D,E,F,G,H,八边形ABCDEFGH即为所求;
(2)由八边形ABCDEFGH是正八边形,求得∠AOD的度数,得到![]() 的长,设这个圆锥底面圆的半径为R,根据圆的周长的公式即可求得结论.
的长,设这个圆锥底面圆的半径为R,根据圆的周长的公式即可求得结论.
试题解析:(1)如图所示,八边形ABCDEFGH即为所求;

(2)∵八边形ABCDEFGH是正八边形,∴∠AOD=![]() ×3=135°,∵OA=5,∴
×3=135°,∵OA=5,∴![]() 的长=
的长=![]() =
=![]() ,设这个圆锥底面圆的半径为R,∴2πR=
,设这个圆锥底面圆的半径为R,∴2πR=![]() ,∴R=
,∴R=![]() ,即这个圆锥底面圆的半径为
,即这个圆锥底面圆的半径为![]() .故答案为:
.故答案为:![]() .
.

练习册系列答案
相关题目