题目内容
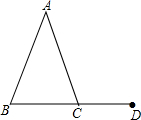
如图,在△ABC中,D为AB边上一点.BD=BC,AD=DC,∠B=36°.求∠ACB的度数.
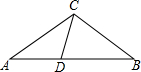

∵BD=BC,∠B=36°,
∴∠BCD=∠BDC=
(180°-∠B)=
(180°-36°)=72°,
∵AD=DC,
∴∠A=∠ACD,
∴∠ACD=
∠BDC=
×72°=36°,
∴∠ACB=∠ACD+∠BCD=36°+72°=108°.
∴∠BCD=∠BDC=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=DC,
∴∠A=∠ACD,
∴∠ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ACB=∠ACD+∠BCD=36°+72°=108°.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目