题目内容
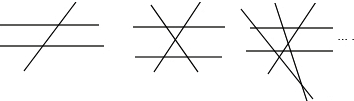
已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )

| A、6 | B、7 | C、8 | D、9 |
分析:首先通过观察图形,找到交点个数与直线条数之间的关系式,然后根据交点个数为27,列出关于n的方程,解方程求出n的值即可.
解答:解:∵当n≥3时,每增加一条直线,交点的个数就增加n-1.即:
当n=3时,共有2个交点;
当n=4时,共有5(=2+3)个交点;
当n=5时,共有9(=5+4)个交点;
…,
∴n条直线共有交点2+3+4+…+(n-1)=
个.
解方程
=27,得n=8或-7(负值舍去).
故选C.
当n=3时,共有2个交点;
当n=4时,共有5(=2+3)个交点;
当n=5时,共有9(=5+4)个交点;
…,
∴n条直线共有交点2+3+4+…+(n-1)=
| n2-n-2 |
| 2 |
解方程
| n2-n-2 |
| 2 |
故选C.
点评:本题考查了平面内直线的交点个数与直线的条数、位置之间的关系,属于竞赛题型,有一定难度.找到用含n的代数式表示交点个数的规律是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 如图,已知∠1,∠2互为补角,且∠3=∠B,
如图,已知∠1,∠2互为补角,且∠3=∠B,