题目内容
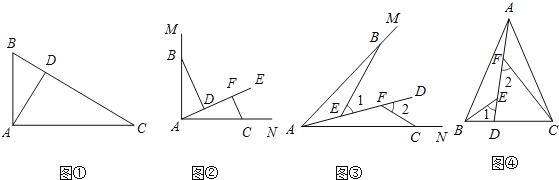
【题目】如图,点M,N分别是∠AOB的边OA,OB上的点,OM=3,ON=7,在∠AOB内有一点G,到边OA,OB的距离相等,且满足GM=GN.
(1)尺规作图:画出点G(要求:保留作图痕迹);
(2)试证明:∠OMG+∠ONG=180°;
(3)若P,Q分别是射线OA,OB上的动点,且满足GP=GQ,则当OP=4时,OQ的长度为 .

【答案】(1)见解析;(2)见解析;(3)4或6
【解析】
(1)作OP平分∠AOB,作线段MN的垂直平分线EF,EF交OP于点G,点G即为所求;
(2)证明△OGK≌△OGH(AAS),推出OK=OH,GK=GH,由GM=GN,∠GKM=∠GHN=90°,推出Rt△GKM≌Rt△GHN(HL),再利用全等三角形的性质,四边形内角和定理解决问题;
(3)首先求出OK=OH=5,PK=1,然后分两种情形分别求解即可解决问题.
解:(1)如图,点G即为所求.
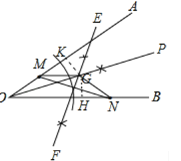
(2)证明:作GK⊥OA于K,GH⊥OB于H.
∵∠GOK=∠GOH,∠GKO=∠GHO=90°,OG=OG,
∴△OGK≌△OGH(AAS),
∴OK=OH,GK=GH,
∵GM=GN,∠GKM=∠GHN=90°,
∴Rt△GKM≌Rt△GHN(HL),
∴∠KGM=∠HGN,
∴∠MGN=∠KGH,
∵∠KGH+∠AOB=180°,
∴∠MGN+∠AOB=180°,
∴∠OMG+∠ONG=180°;
(3)如图,
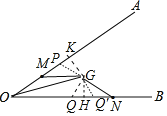
∵OK=OH,MK=NH,
∴OM+ON=OK﹣KM+OH+HN=2OK=10,
∴OK=OH=5,
∵OP=4,
∴PK=5﹣4=1,
∵GP=GQ,
∴当点Q在线段OH上时,OQ=OP=4,
当点Q′在OH的延长线上时,OQ′=5+1=6,
故答案为4或6.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目