题目内容
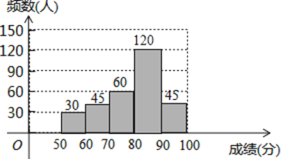
【题目】为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
组别 | 分数段 | 频数(人) | 频率 |
1 | 50≤x<60 | 30 | 0.1 |
2 | 60≤x<70 | 45 | 0.15 |
3 | 70≤x<80 | 60 | n |
4 | 80≤x<90 | m | 0.4 |
5 | 90≤x<100 | 45 | 0.15 |
请根据以图表信息,解答下列问题:
(1)表中m= ,n= ;
(2)补全频数分布直方图;
(3)全体参赛选手成绩的中位数落在第几组;
(4)若得分在80分以上(含80分)的选手可获奖,记者从所有参赛选手中随机采访1人,求这名选手恰好是获奖者的概率.

【答案】(1)120,0.2;(2)详见解析;(3)全体参赛选手成绩的中位数落在80≤x<90这一组;(4)这名选手恰好是获奖者的概率是0.55.
【解析】
(1)根据表格可以求得全体参赛选手的人数,从而可以求得m的值,n的值;
(2)根据(1)中的m的值,可以将补全频数分布直方图;
(3)根据表格可以求得全体参赛选手成绩的中位数落在第几组;
(4)根据表格中的数据可以求得这名选手恰好是获奖者的概率.
解:(1)由表格可得,
全体参赛的选手人数有:30÷0.1=300,
则m=300×0.4=120,n=60÷300=0.2,
故答案为120,0.2;
(2)补全的频数分布直方图如右图所示,
(3)∵35+45=75,75+60=135,135+120=255,
∴全体参赛选手成绩的中位数落在80≤x<90这一组;
(4)由题意可得,
![]() ,
,
即这名选手恰好是获奖者的概率是0.55.

【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.