题目内容
观察、猜想、探究
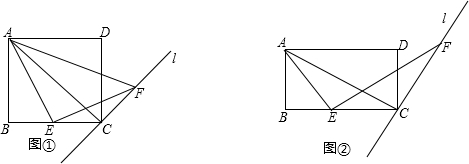
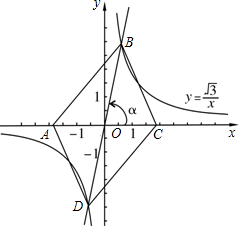
已知矩形ABCD中,直线l垂直AC于点C,点E是BC上的动点(不与点C重合),过点E作EF⊥AE交直线l于点F.
(1)如图①,当AB=BC,E为BC中点时,猜想线段AE与FE有何数量关系,并证明你的猜想;
(2)如图②,已知AB=3,AD=4.
①当点E与点B重合时,求AE:EF的值;
②探究:当点E在线段BC上运动时,AE:EF的值是否发生改变?若不变,请求出该值并给予证明;若发生改变,请说明理由.
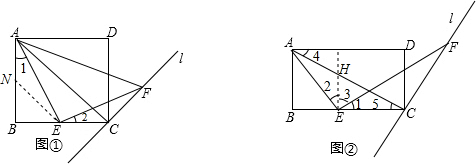 (1)证明:如图(1)当AB=BC,BE=EC,取AB中点N,连接NE,
(1)证明:如图(1)当AB=BC,BE=EC,取AB中点N,连接NE,则AN=EC=NB=BE,
∴∠BNE=∠BEN=45°,∠ANE=135°,
∵AB=BC,∴∠ACB=45°,
∵CF⊥AC,∴∠ACF=90°,
∴∠ECF=∠ACB+∠ACF=135°,
即∠ANE=∠ECF,
∵∠B=90°,
∴∠1+∠AEB=90°,
∵AE⊥EF,
∴∠2+∠AEB=90°,
∴∠1=∠2,
在△ANE和△ECF中,
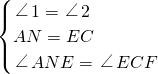 ,
,∴△ANE≌△ECF(ASA),
∴AE=EF;
(2)解:
①当点E与点B重合时,AE与AB重合,EF与BC重合,
AE:EF=AB:BC=3:4;
②比值不变AE:EF=3:4,
证明:如图(2),过点E作EH⊥BC交AC于H,
则∠1+∠3=90°,
∵AE⊥EF,
∴∠2+∠3=90°,
∴∠1=∠2,
∵AD∥BC,
∴∠4=∠5,
∵∠AHE=∠4+90°,∠ECF=∠5+90°,
∴∠AHE=∠ECF,
∴△AEH∽△FEC,
∴
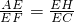 ,
,又∵EH⊥BC,AB⊥BC,
所以
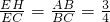 ,
,∴AE:EF=3:4.
分析:(1)当AB=BC,BE=EC,取AB中点N,根据已知得出AN=EC=NB=BE,进而得出∠ANE=∠ECF,∠1=∠2,即可得出△ANE≌△ECF;
(2)①当点E与点B重合时,AE与AB重合,EF与BC重合,得出AE:EF=AB:BC即可得出答案;
②首先过点E作EH⊥BC交AC于H,利用相似三角形的判定得出△AEH∽△FEC,进而求出即可.
点评:此题主要考查了全等三角形的判定与性质以及相似三角形的判定与性质等知识,根据已知得出△AEH∽△FEC是解题关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数
我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数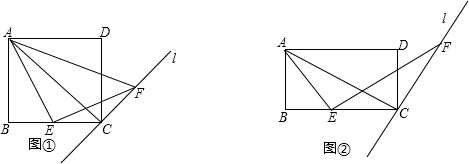

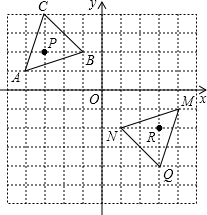 如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经过某种变换后得到的图形.
如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经过某种变换后得到的图形.