��Ŀ����
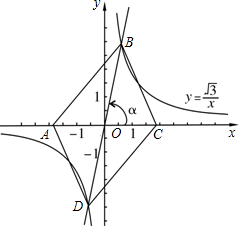 ���������֣�������������ͼ����һ�����ĶԳ�ͼ�Σ������������һ���۽�����⣮��ͼ����ͬһֱ������ϵ�У�������������ͼ����Կ����ǣ���x�����ڵ�ֱ������ԭ��O��ʱ����ת���ȽǺ��ͼ�Σ������뷴��������y=
���������֣�������������ͼ����һ�����ĶԳ�ͼ�Σ������������һ���۽�����⣮��ͼ����ͬһֱ������ϵ�У�������������ͼ����Կ����ǣ���x�����ڵ�ֱ������ԭ��O��ʱ����ת���ȽǺ��ͼ�Σ������뷴��������y=
| ||
| x |
��1��ֱ���жϲ���д�����ۦ�ȡ��ֵ���ı���ABCD����״һ����
��2���ٵ���BΪ��p��1��ʱ���ı���ABCD�Ǿ��Σ�����p��������m��ֵ��
�ڹ۲���룺�Ԣ��е�mֵ����ʹ�ı���ABCDΪ���εĵ�B���м�����������˵����
��3����̽�����ı���ABCD�ܲ��������Σ����ܣ�ֱ��д��B������꣬�����ܣ�˵�����ɣ�
��������1�����ڷ�����������ͼ����һ�����ĶԳ�ͼ�Σ���B��D�������������뷴��������ͼ��Ľ��㣬���Ե�B���D���ڵ�O�����ĶԳƣ���OB=OD����OA=OC�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ��ɵó��ı���ABCD����״��
��2���ٰѵ�B��p��1������y=
���������p��ֵ����B��BE��x����E����Rt��BOE�У��������к����Ķ������tan����ֵ���ó����Ķ�����Ҫ��m��ֵ�����Ƚ�Rt��BOE���ó�OB�ij��ȣ�Ȼ����ݽ��еĶԽ�����ȵó�OA=OB=OC=OD���Ӷ����m��ֵ���ڵ�m=2ʱ����B��x��
������x��0����OB=2���ó�x2+
=4����˷��̣���x=��1���
������������x��ֵ������������ʹ�ı���ABCDΪ���εĵ�B����������
��3�������ı���ABCDΪ���Σ��������εĶԽ��ߴ�ֱ�һ���ƽ�֣���֪AC��BD����AC��BD����ƽ�֣���AC��x���ϣ�����BDӦ��y���ϣ����롰��B��D�ֱ��ڵ�һ�������ޡ�ì�ܣ������ı���ABCD������Ϊ���Σ�
��2���ٰѵ�B��p��1������y=
| ||
| x |
| ||
| x |
| 3 |
| x2 |
| 3 |
��3�������ı���ABCDΪ���Σ��������εĶԽ��ߴ�ֱ�һ���ƽ�֣���֪AC��BD����AC��BD����ƽ�֣���AC��x���ϣ�����BDӦ��y���ϣ����롰��B��D�ֱ��ڵ�һ�������ޡ�ì�ܣ������ı���ABCD������Ϊ���Σ�
���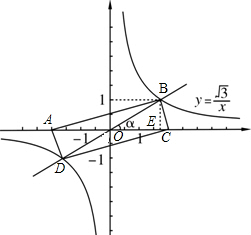 �⣺��1��ƽ���ı��Σ�3�֣�
�⣺��1��ƽ���ı��Σ�3�֣�
��2���١ߵ�B��p��1����y=
��ͼ���ϣ�
��1=
��
��p=
����4�֣�
��B��BE��x����E����OE=
��BE=1
��Rt��BOE��tan��=
=
=
��=30�㣬��5�֣�
��OB=2��
�֡ߵ�B��D�������������뷴��������ͼ��Ľ��㣬
���B��D����ԭ��O�����ĶԳƣ���6�֣�
��OB=OD=2��
���ı���ABCDΪ���Σ���A��-m��0����C��m��0��
��OA=OB=OC=OD=2��7�֣�
��m=2����8�֣�
����ʹ�ı���ABCDΪ���εĵ�B����2������9�֣�
��3���ı���ABCD���������Σ��������£���10�֣�
���ı���ABCDΪ���Σ���Խ���AC��BD����AC��BD����ƽ�֣�
��Ϊ��A��C������ֱ�Ϊ��-m��0������m��0����
���Ե�A��C����ԭ��O�Գƣ���AC��x���ϣ���11�֣�
����BDӦ��y���ϣ�
���롰��B��D�ֱ��ڵ�һ�������ޡ�ì�ܣ�
�����ı���ABCD������Ϊ���Σ���12�֣�
 �⣺��1��ƽ���ı��Σ�3�֣�
�⣺��1��ƽ���ı��Σ�3�֣���2���١ߵ�B��p��1����y=
| ||
| x |
��1=
| ||
| p |
��p=
| 3 |
��B��BE��x����E����OE=
| 3 |
��Rt��BOE��tan��=
| BE |
| OE |
| 1 | ||
|
| ||
| 3 |
��=30�㣬��5�֣�
��OB=2��
�֡ߵ�B��D�������������뷴��������ͼ��Ľ��㣬
���B��D����ԭ��O�����ĶԳƣ���6�֣�
��OB=OD=2��
���ı���ABCDΪ���Σ���A��-m��0����C��m��0��
��OA=OB=OC=OD=2��7�֣�
��m=2����8�֣�
����ʹ�ı���ABCDΪ���εĵ�B����2������9�֣�
��3���ı���ABCD���������Σ��������£���10�֣�
���ı���ABCDΪ���Σ���Խ���AC��BD����AC��BD����ƽ�֣�
��Ϊ��A��C������ֱ�Ϊ��-m��0������m��0����
���Ե�A��C����ԭ��O�Գƣ���AC��x���ϣ���11�֣�
����BDӦ��y���ϣ�
���롰��B��D�ֱ��ڵ�һ�������ޡ�ì�ܣ�
�����ı���ABCD������Ϊ���Σ���12�֣�
������������Ҫ������ƽ���ı��ε��ж������Ρ����ε����ʼ����Ǻ����Ķ����֪ʶ���ۺ��Խ�ǿ���Ѷ����У�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ���������֣�������������ͼ����һ�����ĶԳ�ͼ�Σ������������һ���۽�����⣮��ͼ����ͬһֱ������ϵ�У�������������ͼ����Կ����ǣ���x�����ڵ�ֱ������ԭ��O��ʱ����ת���ȽǺ��ͼ�Σ������뷴��������
���������֣�������������ͼ����һ�����ĶԳ�ͼ�Σ������������һ���۽�����⣮��ͼ����ͬһֱ������ϵ�У�������������ͼ����Կ����ǣ���x�����ڵ�ֱ������ԭ��O��ʱ����ת���ȽǺ��ͼ�Σ������뷴�������� �Ⱥ��ͼ�Ρ����뷴��������
�Ⱥ��ͼ�Ρ����뷴�������� ��ͼ��ֱ��ڵ�һ�������ĵ�B��D����֪��A��-m��0����C��m��0����
��ͼ��ֱ��ڵ�һ�������ĵ�B��D����֪��A��-m��0����C��m��0����
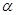 �Ⱥ��ͼ�Ρ����뷴��������
�Ⱥ��ͼ�Ρ����뷴�������� ��ͼ��ֱ��ڵ�һ�������ĵ�B��D����֪��A��-m��0����C��m��0����
��ͼ��ֱ��ڵ�һ�������ĵ�B��D����֪��A��-m��0����C��m��0����
 ��ͼ��ֱ��ڵ�һ�������ĵ�B��D����֪��A��-m��0����C��m��0����
��ͼ��ֱ��ڵ�һ�������ĵ�B��D����֪��A��-m��0����C��m��0����