题目内容
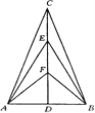
【题目】如图，在△ABC中，AC=BC，CD是AB边上的高线，且有2CD=3AB，又E，F为CD的三等分点，则∠ACB与∠AEB之和为（ ）
A. 45° B. 90° C. 75° D. 135°
【答案】B
【解析】
根据等腰三角形三线合一的特点可知：CD垂直平分AB，利用线段之间的关系，得到△DBF是等腰直角三角形；再利用勾股定理求得BF、BD的关系，可得到
=
，接下来结合夹角相等证明△EFB∽△BFC，联系相似三角形的性质及三角形外角的性质即可得出结论.
设AD=x，
∵AC=BC，CD是AB边上的高，
∴CD是AB的垂直平分线，CD平分∠ACB，ED平分∠AEB，
∴BD=AD=x，AE=BE，AF=BF，∠ACB=2∠FCB，∠AEB=2∠FEB.
∵2CD=3AB，AD=BD=x，E、F是三等分点，
∴CD=3x，DF=EF=CE=DB=x.
又∵∠CDB=90°，
∴△DBF是等腰三角形，
∴∠DBF=45°，BF=
x，
∴
，
，
∴=.
又∵∠EFB=∠BFC，
∴△EFB∽△BFC，
∴∠FBE=∠BCF，∠FEB=∠FBC.
∴∠DFB=∠FBE+∠FEB=∠FCB+∠FBC=45°，
∴∠ACB+∠AEB=2(∠FBE+∠FEB)=90°.
故选B.
练习册系列答案
相关题目
【题目】一水池中有水
，如果每分钟放出
的水，水池里的水量与放水时间有如下关系：
放水时间（分） | 1 | 2 | 3 | 4 | … |
水池中水量 | 38 | 36 | 34 | 32 | … |
下列数据中满足此表格的是（ ）
A.放水时间8分钟，水池中水量
B.放水时间20分钟，水池中水量
C.放水时间26分钟，水池中水量
D.放水时间18分钟，水池中水量
