题目内容
(2013•香坊区一模)已知E为△ABC内部一点,AE延长线交边BC于点D,连接BE、CE,∠BED=∠BAC=2∠DEC.
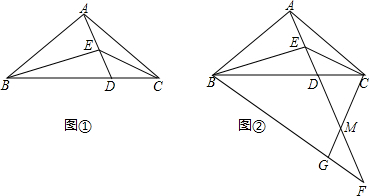
(1)如图①,若AC=AB,求证:BE=2AE;
(2)如图②,在(1)的条件下,将∠ABC沿BC翻折得到∠FBC,AE延长线经过点F,M为DF的中点,连接CM并延长交BF于点G.若CG=3
,AE=2DE,求BD的长.

(1)如图①,若AC=AB,求证:BE=2AE;
(2)如图②,在(1)的条件下,将∠ABC沿BC翻折得到∠FBC,AE延长线经过点F,M为DF的中点,连接CM并延长交BF于点G.若CG=3
| 2 |
分析:(1)在EB上截取EF=AE,利用AAS即可证得△ABF≌△CAE,根据全等三角形的对应边相等即可证得;
(2)首先证明△ADC∽△FDB,即可证得△ABE∽△AFB,利用相似三角形的对应边的比相等利用a表示出AB的长,过A作AH⊥BC于H,连接CF,可以证明△ABH∽△FBC,则∠FCB=90°,从而求得AB的长,过C作CK⊥DF于K,设MK=x,证明△ADH∽△CDK,根据相似三角形的对应边的比相等即可求得CD、BD的长.
(2)首先证明△ADC∽△FDB,即可证得△ABE∽△AFB,利用相似三角形的对应边的比相等利用a表示出AB的长,过A作AH⊥BC于H,连接CF,可以证明△ABH∽△FBC,则∠FCB=90°,从而求得AB的长,过C作CK⊥DF于K,设MK=x,证明△ADH∽△CDK,根据相似三角形的对应边的比相等即可求得CD、BD的长.
解答: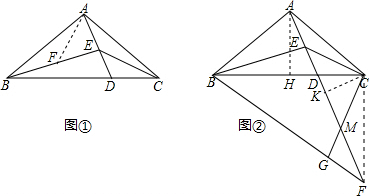 解:(1)在EB上截取EF=AE,设∠BED=2α,
解:(1)在EB上截取EF=AE,设∠BED=2α,
∴∠FAE=∠AFE=α,
∴∠AEC=∠AFB,
∵∠CAD+∠BAD=∠BAC=2α,∠ABE+∠BAD=∠BED=2α,
∴∠CAE=∠ABE
∵在△ABF和△CAE中,
,
∴△ABF≌△CAE(AAS),
∴BF=AE=EF,
∴BE=2AE,
(2)∵AB=AC,
∴∠ABC=∠ACB,
又∵∠ABC=∠CBF,
∴∠ACB=∠CBF,
∴AC∥FB,
∴∠AFB=∠CAE,
∵∠ADC=∠BDF,
∴△ADC∽△FDB,由(1)知,∠CAE=∠ABE,
∴∠ABE=∠AFB,
∵∠BAF=∠BAF,
∴△ABE∽△AFB,
∴
=
,
=
,
由(1)知,BE=2AE,
∴BF=2AB,
∴BF=2AC,BD=2DC
∴DF=2AD,设AE=2a,
则DE=a,DM=MF=3a,
∴
=
=2
∴CM=2GM=2
∴AB2=AE•AF=18a,
∴AB=3
a,
过A作AH⊥BC于H,连接CF,
∵∠ABH=∠FBC,
=
=2,
∴△ABH∽△FBC,
∴∠FCB=90°,
∴CM=DM=3a=2
,
∴a=
,
∴AB=3
a=4,
过C作CK⊥DF于K,设MK=x,
∴CM2-KM2=AC2-AK2,
∴(2
)2-x2=42-(4
-x)2,
∴x=
,
∴DK=
,
∵∠ADB=∠CDK,∠AHD=∠CKD,
∴△ADH∽△CDK,
∴
=
∵BD=2DC,BH=HC,
∴HD=
CD,
∴
=
,
∴CD=2,BD=4.
 解:(1)在EB上截取EF=AE,设∠BED=2α,
解:(1)在EB上截取EF=AE,设∠BED=2α,∴∠FAE=∠AFE=α,
∴∠AEC=∠AFB,
∵∠CAD+∠BAD=∠BAC=2α,∠ABE+∠BAD=∠BED=2α,
∴∠CAE=∠ABE
∵在△ABF和△CAE中,
|
∴△ABF≌△CAE(AAS),
∴BF=AE=EF,
∴BE=2AE,
(2)∵AB=AC,
∴∠ABC=∠ACB,
又∵∠ABC=∠CBF,
∴∠ACB=∠CBF,
∴AC∥FB,
∴∠AFB=∠CAE,
∵∠ADC=∠BDF,
∴△ADC∽△FDB,由(1)知,∠CAE=∠ABE,
∴∠ABE=∠AFB,
∵∠BAF=∠BAF,
∴△ABE∽△AFB,
∴
| AB |
| AE |
| AF |
| AB |
| BE |
| BF |
| AE |
| AB |
由(1)知,BE=2AE,
∴BF=2AB,
∴BF=2AC,BD=2DC
∴DF=2AD,设AE=2a,
则DE=a,DM=MF=3a,
∴
| AM |
| MF |
| CM |
| MG |
∴CM=2GM=2
| 2 |
∴AB2=AE•AF=18a,
∴AB=3
| 2 |
过A作AH⊥BC于H,连接CF,
∵∠ABH=∠FBC,
| BC |
| AH |
| BF |
| AB |
∴△ABH∽△FBC,
∴∠FCB=90°,
∴CM=DM=3a=2
| 2 |
∴a=
2
| ||
| 3 |
∴AB=3
| 2 |
过C作CK⊥DF于K,设MK=x,
∴CM2-KM2=AC2-AK2,
∴(2
| 2 |
| 2 |
∴x=
3
| ||
| 2 |
∴DK=
| ||
| 2 |
∵∠ADB=∠CDK,∠AHD=∠CKD,
∴△ADH∽△CDK,
∴
| AD |
| CD |
| HD |
| DK |
∵BD=2DC,BH=HC,
∴HD=
| 1 |
| 2 |
∴
2
| ||
| CD |
| ||||
|
∴CD=2,BD=4.
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,正确利用相似三角形的性质对线段的比进行变化是关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

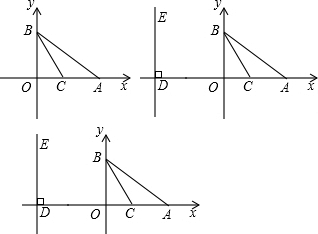 (2013•香坊区一模)如图,在平面直角坐标系中,点O为坐标原点,直线y=
(2013•香坊区一模)如图,在平面直角坐标系中,点O为坐标原点,直线y=