题目内容
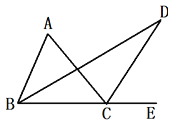
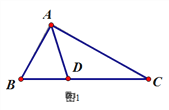
【题目】徐老师给爱好学习的小敏和小捷提出这样一个问题:如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
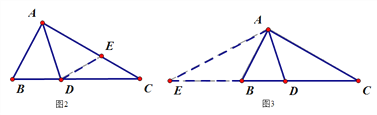
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)请你任意选择一种思路继续完成下一步的证明.
【答案】答案见解析
【解析】试题分析:小敏的方法是利用角平分线添加辅助线,构造全等三角形,△ABD和△AED证明AB+BD=AC.小捷的方法构造等腰三角形AEC,EAD,证明AB+BD=AC.
试题解析:
小敏的证明思路是:如图2,在AC上截取AE=AB,连接DE.(如图2)
∵AD是∠BAC的平分线,
∴∠BAD=∠EAD,
在△ABD和△AED中,
AB=AE,
∠BAD=∠EAD,
AD=AD,
∴△ABD≌△AED(SAS),
∴BD=DE,∠ABD=∠AED,
∵∠AED=∠EDC+∠C,∠B=2∠C,
∴∠EDC=∠C,
∴DE=EC,即AB+BD=AC;
小捷的证明思路是:如图3,延长CB至点E,使BE=AB,连接AE.
∴∠E=∠BAE,
∵∠ABC=∠E+∠BAE,
∴∠ABC=2∠E,
∵∠ABC=2∠C,
∴∠E=∠C,
∴△AEC是等腰三角形,
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC,
∵∠ADE=∠DAC+∠C,∠DAE=∠BAD+∠BAE,
∴∠ADE=∠DAE,
∴EA=ED=AC,
∴AB+BD=AC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目