Question

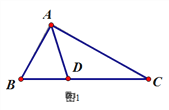
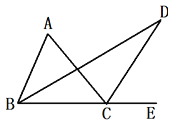
【题目】在ΔABC中，∠ABC的平分线与在∠ACE的平分线相交于点D．

（1）若∠ABC=60°，∠ACB=40°，求∠A和∠D的度数．

（2）由（1）小题的计算结果，猜想，∠A和∠D有什么数量关系，并加以证明．

Answer 1

【答案】答案见解析

【解析】试题分析：（1）根据三角形内角和定理和角平分线的性质，已知∠ABC=60°，∠ACB=40°，易求∠A和∠D度数．（2）根据三角形外角的性质以及角平分线性质，可得∠ACE=2∠D+∠ABC，∠ACE=∠A+∠ABC，即可得∠A和∠D的数量关系．

试题解析：解：（1）∵∠ABC＝60°，∠ACB＝40°，∴∠A＝80°．

∵BD平分∠ABC，∠ABC＝60°，

∴∠DBC＝30°．

又∵∠ACB＝40°，

∴∠ACE＝140°．

又∵CD是∠ACE的平分线，

∴∠DCE＝70°．

∴∠D＝40°

（2）∠A=2∠D．

证明：∵CD 平分∠ACE

∴∠ACE=2∠DCE

又∠DCE=∠D+∠DBC

∴2∠DCE=2∠D+2∠DBC

∵BD平分∠ABC

∴∠ABC=2∠DBC

即∠ACE=2∠D+∠ABC

而∠ACE=∠A+∠ABC

∴2∠D=∠A