题目内容
在平面直角坐标系中,图①和图②中的各三角形顶点均在网格图的格点上,根据所给信息解答下列问题:
(1)动手操作,探究结论:在图①中,△ABO的三个顶点的坐标分别是A(2,4)、B(4,0)、O(0,0),将△ABO的三个顶点的横坐标都加上2,纵坐标不变,分别得到点A’、B’、O’,依次连接A’、B’、O’各点,画出△A’B’O’,并说明△A’B’O’与△ABO在大小、形状、位置上有什么关系?
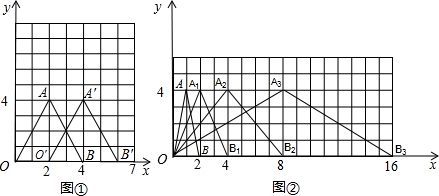
(2)仔细观察,探究规律:在图②中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0)B2(8,0),B3(16,0)…
①按此图形变化规律,写出△OA4B4的顶点坐标A4______,B4______;
②通过计算得出△OA4B4的面积是△OAB面积的______倍;
③通过上述变化规律,请你猜想出△OAnBn的面积是△OAB面积的多少倍?
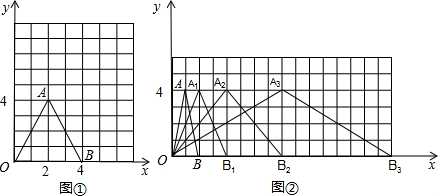
解:(1)如图,△A′B′O′与△ABO的形状,大小完全相同,△A′B′O′可以看作将△ABO向右平移2个单位得到的;
(2)①8×2=16,16×2=32,
∴A4(16,4)、B4(32,0),
②∵△OA4B4与△OAB的高都是4,OB4=16×2=32,OB=2,
∴S△OA4B4=
 ×32×4=64,
×32×4=64,S△OAB=
 ×2×4=4,
×2×4=4,64÷4=16,
∴△OA4B4的面积是△OAB面积的16倍;
③根据规律,后一个三角形的底边是前一个三角形底边的2倍,高相等都是4,
∴OBn=2n+1,
S△OAnBn=
 ×2n+1×4=2n+2,
×2n+1×4=2n+2,S△OAB=
 ×2×4=4,
×2×4=4,2n+2÷4=2n,
∴△OAnBn的面积是△OAB面积的2n倍.
分析:(1)把点A、B、C向右移动两个单位,分别找出点A′、B′、O′的位置,然后顺次连接即可得到△A′B′O′,然后根据平移的性质解答;
(2)①根据规律发现,把点A3与点B3的横坐标扩大2倍,纵坐标不变解答;
②根据三角形的面积公式分别计算出△OA4B4的面积与△OAB的面积,然后相除即可求出倍数;
③根据三角形的底边后一个是前一个三角形的底边的2倍,先求出△OAnBn的底边OBn的长度,高都是4不变,然后利用三角形的面积公式分别计算出两三角形的面积,相除即可得到倍数.
点评:本题考查了坐标变换的平移变换以及图形规律的探寻,(2)中发现三角形的高都是4不变,底边成2倍扩大的规律是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
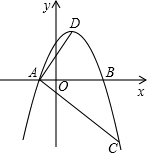 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=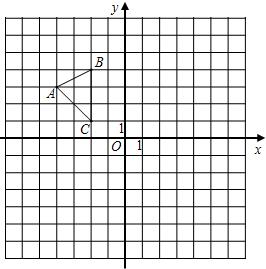 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.