题目内容
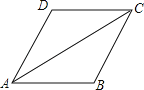
【题目】(10分)如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是 .
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,请说明理由.

【答案】(1)50°.(2)①6cm; ②存在,周长最小值为14cm
【解析】(1)50°.
(2)①∵AN=BN,
∴BN+CN=AN+CN=AC,
∵AB=AC=8cm,
∴BN+CN=8cm,
∵△NBC的周长是14cm.
∴BC=14﹣8=6cm.
②∵A、B关于直线MN对称,
∴连接AC与MN的交点即为所求的P点,此时P和N重合,
即△BNC的周长就是△PBC的周长最小值,
∴△PBC的周长最小值为14cm.

练习册系列答案
相关题目
【题目】在一次课外学习中,小丁先画出图(1)所示的等边三角形,然后依次取各边中点并连接成图(2)、图(3). 那么在第1个图形中有1个三角形,第2个图形中共有5个三角形,……,第n个图形中共有m个三角形.
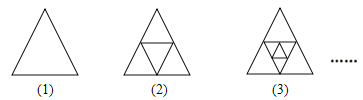
观察图形,填写下面的表格:
n | 1 | 2 | 3 | 4 | 5 | 6 | …… |
m | 1 | 5 |
(2)在研究的过程中,小丁发现,图形中三角形的总个数m与图形的序号n之间满足一次函数关系,试求出m与n的函数关系式,并指出自变量的取值范围.
(3)在进一步研究中小丁发现,当n=![]() 时,m的值与k的值有关,试直接写出m与k的关系式.
时,m的值与k的值有关,试直接写出m与k的关系式.