Question

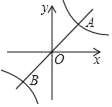
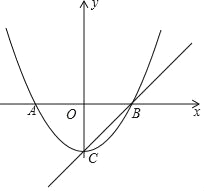
【题目】如图，已知顶点为C（0，﹣3）的抛物线y＝ax2+b（a≠0）与x轴交于A，B两点，直线y＝x+m过顶点C和点B．

（I）求点B的坐标；

（Ⅱ）求二次函数y＝ax2+b（a≠0）的解析式；

（Ⅲ）抛物线y＝ax2+b（a≠0）上是否存在点M，使得∠MCB＝15°？若存在，求出点M的坐标；若不存在，请说明理由．

Answer 1

【答案】（I）（3，0）；（Ⅱ）y＝；（Ⅲ）（3，6）或（，﹣2）．

【解析】

（Ⅰ）根据点C（0，﹣3），直线y＝x+m过点C和点B，可以求得直线的解析式，从而可以求得点B的坐标；

（Ⅱ）根据点B和点C的坐标可以求得二次函数的解析式；

（Ⅲ）根据题意，可以画出相应的图形，然后根据二次函数的性质和锐角三角函数可以求得点M的坐标．

解：（Ⅰ）∵点C（0，﹣3），直线y＝x+m过点C和点B，

∴﹣3＝0+m，得m＝﹣3，

∴y＝x﹣3，

当y＝0时，0＝x﹣3，得x＝3，

∴点B的坐标为（3，0）；

（Ⅱ）∵抛物线y＝ax2+b过点B（3，0），点C（0，﹣3），

∴，得，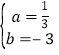

∴抛物线的解析式为y＝；

（Ⅲ）抛物线y＝ax2+b（a≠0）上存在点M，使得∠MCB＝15°，

∵点B（3，0），点C（0，﹣3），

∴OC＝OB＝3，

∵∠BOC＝90°，

∴∠OCB＝∠OBC＝45°，

当∠M1CB＝15°时，设点M1的坐标为（m1，），

则∠M1CO＝30°，

∴，

解得，m1＝3或m1＝0（舍去），

当m1＝3时，﹣3＝6，

即点M1的坐标为（3，6）；

当M2CB＝15°时，设点M2的坐标为（m2，），

则∠M2CO＝60°，

∴，

解得，m2＝或m2＝0（舍去），

当m2＝时，＝﹣2，

即点M2的坐标为（，﹣2）；

由上可得，点M的坐标为（3，6）或（，﹣2）．