题目内容
【题目】如图,A(3,3)、C(0,2),点B(b,0)是x轴正半轴上一动点,点D是点A关于x轴的对称点.
(1)写出点D的坐标并用b表示四边形AODB的面积S;
(2)连结CD交x轴于P,试求AP与CP的和;
(3)在点B从左向右移动过程中,点B处于哪些位置时△OBD是特殊的三角形?写出点B的坐标并分别说明理由.
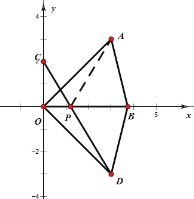
【答案】(1)![]() ,S=3b;(2)AP+CP=
,S=3b;(2)AP+CP=![]() ;(3)当点B处于(3,0)和(6,0)时,△OBD是特殊的三角形,理由见解析
;(3)当点B处于(3,0)和(6,0)时,△OBD是特殊的三角形,理由见解析
【解析】
(1)根据两点关于x轴对称的特征即可确定点D的坐标,再根据四边形AODB的面积等于2S△AOB求解即可;
(2)根据“两点之间线段最短”进行求解即可;
(3)依据等腰三角形和等腰直角三角形的定义结合已知条件进行判断即可.
(1)∵点D是点A关于x轴的对称点
∴D(3,-3)
由已知可得△OBD和△AOB关于x轴对称
∴S= 2S△AOB=![]() =3b.
=3b.
(2)如图,
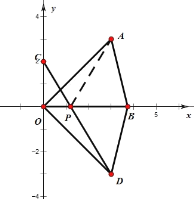
由已知和(1)可得,AP=PD
又CD=![]() =
=![]()
∴AP+CP=CD=![]() ;
;
(3)当点B处于(3,0),(![]() ,0)和(6,0)时,△OBD是特殊的三角形.理由如下:
,0)和(6,0)时,△OBD是特殊的三角形.理由如下:
∵D(3,-3)
∴∠DOB=45°
①当 B处于(3,0)时,△OBD是等腰直角三角形,且∠OBD=90°;
②当 B处于(6,0)时,△OBD是等腰直角三角形,且∠ODB=90°;
③当 B处于(![]() ,0)时,△OBD是等腰三角形,且OD=OB;
,0)时,△OBD是等腰三角形,且OD=OB;

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目