��Ŀ����
��ͼ����ֱ������ABCD�У�AD��BC����C=90�㣬BC=16��DC=12��AD=21������P�ӵ�D������������DA�ķ���������DA����ÿ��2������λ�����ٶ��˶�������Q�ӵ�C���������߶�CB����ÿ��1����λ�����ٶ����B�˶�����P��Q�ֱ�ӵ�D��Cͬʱ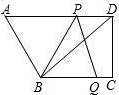 ����������Q�˶�����Bʱ����P��ֹ֮ͣ�˶������˶���ʱ��Ϊt���룩��
����������Q�˶�����Bʱ����P��ֹ֮ͣ�˶������˶���ʱ��Ϊt���룩����1�����BPQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��2����tΪ��ֵʱ����B��P��Q����Ϊ������������ǵ��������Σ�
��3�����߶�PQ���߶�AB�ཻ�ڵ�O����2AO=OBʱ�����BQP������ֵ��
��4���Ƿ����ʱ��t��ʹ��PQ��BD�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��������1����P��PM��BC������ΪM�����ı���PDCMΪ���Σ��������ε������ʽ�Ϳ�������t��ʾ���͵õ�S��t֮��ĺ�����ϵʽ��
��2����B��P��Q����Ϊ������������ǵ��������Σ����Է����������
����PQ=BQ������BP=BQ������PB=PQ��
��Rt��PMQ�и��ݹ��ɶ������͵õ�һ������t�ķ��̣��Ϳ������t��
��3���������������ζ�Ӧ�߳ɱ�������ʽ���t���Ӷ��������еĶ������ֵ��
��4�����ȼ�����ڣ�Ȼ���ٸ������������ζ�Ӧ�߳ɱ�����֤��
��2����B��P��Q����Ϊ������������ǵ��������Σ����Է����������
����PQ=BQ������BP=BQ������PB=PQ��
��Rt��PMQ�и��ݹ��ɶ������͵õ�һ������t�ķ��̣��Ϳ������t��
��3���������������ζ�Ӧ�߳ɱ�������ʽ���t���Ӷ��������еĶ������ֵ��
��4�����ȼ�����ڣ�Ȼ���ٸ������������ζ�Ӧ�߳ɱ�����֤��
���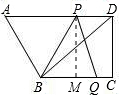 �⣺��1����ͼ������P��PM��BC������ΪM�����ı���PDCMΪ���Σ�
�⣺��1����ͼ������P��PM��BC������ΪM�����ı���PDCMΪ���Σ�
��PM=DC=12��
��QB=16-t��
��S=
��12����16-t��=96-6t��0��t��16����
��2����ͼ��֪��CM=PD=2t��CQ=t��
��B��P��Q����Ϊ������������ǵ��������Σ����Է����������
����PQ=BQ��
��Rt��PMQ��PQ2=t2+122��
��PQ2=BQ2��t2+122=��16-t��2��
���t=
��
����BP=BQ��
��Rt��PMB��BP2=��16-2t��2+122��
��BP2=BQ2���16-2t��2+122=��16-t��2
��3t2-32t+144=0��
���ڡ�=-704��0��
��3t2-32t+144=0�⣬
��PB��BQ��
����PB=PQ��
��PB2=PQ2����t2+122=��16-2t��2+122
��������3t2-64t+256=0��
���t1=
��t2=16����ȥ��
�ۺ���������ۿ�֪����t=
���t=
��ʱ����B��P��Q����Ϊ������������ǵ��������Σ�
��3����ͼ���ɡ�OAP�ס�OBQ����
=
=
��
 ��AP=2t-21��BQ=16-t��
��AP=2t-21��BQ=16-t��
��2��2t-21��=16-t��
��t=
��
����Q��QE��AD������ΪE��
��PD=2t��ED=QC=t��
��PE=t��
��Rt��PEQ��tan��QPE=
=
=
��
�֡�AD��BC��
���BQP=��QPE��
��tan��BQP=
��
��4�������ʱ��t��ʹ��PQ��BD��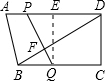
��ͼ������Q��QE��AD��E������ΪE��
��AD��BC
���BQF=��EPQ��
�֡��ڡ�BFQ�͡�BCD�С�BFQ=��C=90�㣬
���BQF=��BDC��
���BDC=��EPQ��
�֡ߡ�C=��PEQ=90�㣬
��Rt��BDC��Rt��QPE��
��
=
����
=
��
���t=9��
���ԣ���t=9��ʱ��PQ��BD��
 �⣺��1����ͼ������P��PM��BC������ΪM�����ı���PDCMΪ���Σ�
�⣺��1����ͼ������P��PM��BC������ΪM�����ı���PDCMΪ���Σ���PM=DC=12��
��QB=16-t��
��S=
| 1 |
| 2 |
��2����ͼ��֪��CM=PD=2t��CQ=t��
��B��P��Q����Ϊ������������ǵ��������Σ����Է����������
����PQ=BQ��
��Rt��PMQ��PQ2=t2+122��
��PQ2=BQ2��t2+122=��16-t��2��
���t=
| 7 |
| 2 |
����BP=BQ��
��Rt��PMB��BP2=��16-2t��2+122��
��BP2=BQ2���16-2t��2+122=��16-t��2
��3t2-32t+144=0��
���ڡ�=-704��0��
��3t2-32t+144=0�⣬
��PB��BQ��
����PB=PQ��
��PB2=PQ2����t2+122=��16-2t��2+122
��������3t2-64t+256=0��
���t1=
| 16 |
| 3 |
�ۺ���������ۿ�֪����t=
| 7 |
| 2 |
| 16 |
| 3 |
��3����ͼ���ɡ�OAP�ס�OBQ����
| AP |
| BQ |
| AO |
| OB |
| 1 |
| 2 |
 ��AP=2t-21��BQ=16-t��
��AP=2t-21��BQ=16-t����2��2t-21��=16-t��
��t=
| 58 |
| 5 |
����Q��QE��AD������ΪE��
��PD=2t��ED=QC=t��
��PE=t��
��Rt��PEQ��tan��QPE=
| QE |
| PE |
| 12 |
| t |
| 30 |
| 29 |
�֡�AD��BC��
���BQP=��QPE��
��tan��BQP=
| 30 |
| 29 |
��4�������ʱ��t��ʹ��PQ��BD��

��ͼ������Q��QE��AD��E������ΪE��
��AD��BC
���BQF=��EPQ��
�֡��ڡ�BFQ�͡�BCD�С�BFQ=��C=90�㣬
���BQF=��BDC��
���BDC=��EPQ��
�֡ߡ�C=��PEQ=90�㣬
��Rt��BDC��Rt��QPE��
��
| DC |
| BC |
| PE |
| EQ |
| 12 |
| 16 |
| t |
| 12 |
���t=9��
���ԣ���t=9��ʱ��PQ��BD��
���������ε��������ͨ�������߿���ת��Ϊֱ������������ε����⣮����Ҫ������B��P��Q����Ϊ������������ǵ��������Σ�Ӧ�֢���PQ=BQ������BP=BQ������PB=PQ����������������ۣ�

��ϰ��ϵ�д�
�����Ŀ
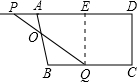
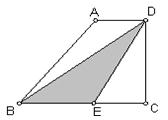 20����ͼ����ֱ������ABCD�У�AD��BC��CD��BC��EΪBC���ϵĵ㣮��ֱ������ABCD�ضԽ���BD�۵���ʹ��ABD���EBD�غϣ���ͼ����Ӱ��ʾ��������A=130�㣬AB=4cm��������ABCD�ĸ�CD��
20����ͼ����ֱ������ABCD�У�AD��BC��CD��BC��EΪBC���ϵĵ㣮��ֱ������ABCD�ضԽ���BD�۵���ʹ��ABD���EBD�غϣ���ͼ����Ӱ��ʾ��������A=130�㣬AB=4cm��������ABCD�ĸ�CD��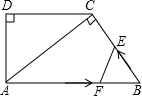 ��ͼ����ֱ������ABCD�У�AB��DC����D=90�㣬AC��BC��AB=10cm��BC=6cm��F����2cm/����ٶ����߶�AB����A��B�����˶���E��ͬʱ��1cm/����ٶ����߶�BC����B��C�����˶������˶�ʱ��Ϊt�루0��t��5����
��ͼ����ֱ������ABCD�У�AB��DC����D=90�㣬AC��BC��AB=10cm��BC=6cm��F����2cm/����ٶ����߶�AB����A��B�����˶���E��ͬʱ��1cm/����ٶ����߶�BC����B��C�����˶������˶�ʱ��Ϊt�루0��t��5����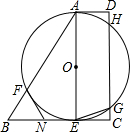 ��1998•��������ͼ����ֱ������ABCD�У�AD��BC��DC��BC����BC=3AD�������εĸ�AEΪֱ���ġ�O��AB�ڵ�F����CD�ڵ�G��H������F����O�����߽�BC�ڵ�N��
��1998•��������ͼ����ֱ������ABCD�У�AD��BC��DC��BC����BC=3AD�������εĸ�AEΪֱ���ġ�O��AB�ڵ�F����CD�ڵ�G��H������F����O�����߽�BC�ڵ�N�� BC�ϵĶ��㣬��G��AB�ϣ����ı���AEFG�Ǿ��Σ���FG=x������AEFG�����Ϊy��
BC�ϵĶ��㣬��G��AB�ϣ����ı���AEFG�Ǿ��Σ���FG=x������AEFG�����Ϊy��