题目内容
【题目】2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线![]() 和x轴上,则第n个阴影正方形的面积为
和x轴上,则第n个阴影正方形的面积为 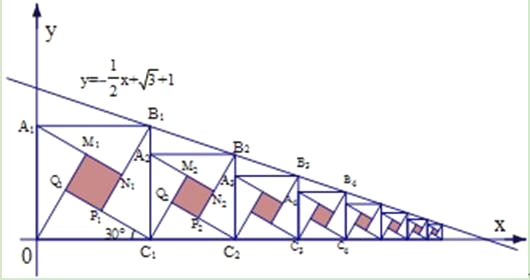
【答案】2×(![]() )n
)n
【解析】
∵B1点坐标设为(t,t),
∴t=﹣![]() t+
t+![]() +1,
+1,
解得:t=![]() (
(![]() ),
),
如果B1N1=a,那么大正方形边长为2a,阴影正方形边长为(![]() ﹣1)a,
﹣1)a,
∴可以理解成是一系列的相似多边形,相似比为2:3,
∴第2个阴影正方形的面积为:(![]() )×
)×![]() (
(![]() +1)=
+1)=![]() ,
,
第3个阴影正方形的面积为:(![]() ﹣1)×
﹣1)×![]() (
(![]() )=
)=![]() ,
,
∴第n个阴影正方形的面积为:(![]() ﹣1)×(
﹣1)×(![]() )n(
)n(![]() +1)=2×(
+1)=2×(![]() )n,
)n,
故答案为:2×(![]() )n.
)n.

练习册系列答案
相关题目
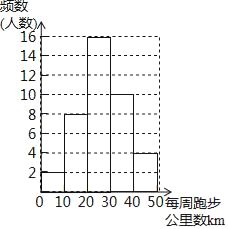
【题目】某市举行主题为“奔跑吧!2018”的市民健康跑活动.红树林学校的小记者随机采访了40名参赛选手,了解到他们平时每周跑步公里数(单位:km),并根据统计结果绘制出以下频数分布直方图和不完整的表格.
每周跑步公里数/km | 频数(人数) | 频率 |
0≤x<10 | 2 | 5% |
10≤x<20 | a | m |
20≤x<30 | b | 40% |
30≤x<40 | 10 | 25% |
40≤x<50 | 4 | n |
(1)求a= ,n= ;
(2)本次活动有10000人参加比赛,请根据上述调查结果,估算该活动中每周跑步公里数在10≤x<30 内的人数;
(3)应比赛组委会要求,现从每周跑步公里数在40≤x<50 内的4名参赛选手甲,乙,丙,丁中随机抽取2人作为本次活动的形象宣传员,请用画树状图法或列表法求出恰好抽中乙,丙两人的概率.