题目内容
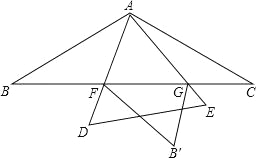
【题目】如图，△ABC中，AB=AC=4，∠BAC=120°，以A为一个顶点的等边三角形ADE绕点A在∠BAC内旋转，AD、AE所在的直线与BC边分别交于点F、G．若点B关于直线AD的对称点为B′，当△FGB′是以点G为直角顶点的直角三角形时，BF的长为 ．
【答案】4
﹣4
【解析】
试题分析：作AH⊥BC于H，如图1，先根据等腰三角形的性质和含30度的直角三角形三边的关系求出BC=4，再把△ACG绕点A顺时针旋转120°得到△ABG′，连结FG′、AB′，如图，则根据旋转的性质得BG′=CG，AG=AG，∠ABG′=∠C=30°，∠1=∠BAG′，所以∠FBG′=60°，再证明△AFG≌△AFG′得到FG=FG′，接着利用对称性质得FB=FB′，AB=AB′，∠2=∠3，易得∠1=∠4，AC=AB′，则可判断△AB′G与△ACG关于AG对称，得到GB′=GC，则GB′=BG′，然后证明△FB′G≌△FBG′得到∠FGB′=∠BG′F=90°，于是在Rt△BFG′中含30度的直角三角形三边的关系得BG′=
BF，FG′=
BF，则BF+
BF+
BF=BC=4
，然后解关于BF的方程即可．
练习册系列答案
相关题目
