Question

【题目】如图，△ABC中，∠B=60°，∠C=75°，AC=3 ，求AB的长．

Answer 1

【答案】解：过点C作CD⊥AB于点D，
∵∠B=60°，∠C=75°，
∴∠A=45°，
在△ADC中，AC=3 ，
∵sinA= ，
∴AD=sin45°×3 =3=CD，
在△BDC中，∠DCB=30°，
∵ctgB=
∴BD=cot60°×3= ，
∴AB= +3，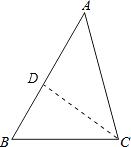

【解析】过点C作CD⊥AB于点D，先根据三角形内角和定理计算出∠A=45°，在Rt△ADC中，利用∠A的正弦可计算出CD，进而求得AD，然后在Rt△BDC中，利用∠B的余切可计算出BD，进而就可求得AB．
【考点精析】掌握三角形的内角和外角是解答本题的根本，需要知道三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．