题目内容
如图，等腰梯形ABCD下底与上底的差恰好等于腰长，则∠C=（ ）| A、75° | B、60° | C、45° | D、30° |
分析：过点A作AE⊥BC，垂足为E，过点D作DF⊥BC，垂足为F，根据等腰梯形的性质可知BE=
AB，再根据含30度角的直角三角形的性质，即可求出答案．
| 1 |
| 2 |
解答：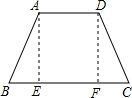
解：过点A作AE⊥BC，垂足为E，过点D作DF⊥BC，垂足为F，
∵等腰梯形ABCD下底与上底的差恰好等于腰长，
∴BE+CF=AB，
又BE=CF，
∴BE=
AB，
根据含30度角的直角三角形的性质，可知∠B=60°，
∴∠C=∠B=60°．
故选B．
解：过点A作AE⊥BC，垂足为E，过点D作DF⊥BC，垂足为F，∵等腰梯形ABCD下底与上底的差恰好等于腰长，
∴BE+CF=AB，
又BE=CF，
∴BE=
| 1 |
| 2 |
根据含30度角的直角三角形的性质，可知∠B=60°，
∴∠C=∠B=60°．
故选B．
点评：本题考查等腰梯形的性质，难度适中，解题关键是掌握等腰梯形的两底角相等．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
14、如图，等腰梯形ABCD中，AB∥CD，∠A=60°，BD平分∠ABC，若梯形ABCD的周长为40cm，则CD的长为（ ）
24、已知：如图，等腰梯形ABCD中，AD∥BC，BD平分∠ABC．
（2007•昌平区二模）已知：如图，等腰梯形ABCD中，AD∥BC，BD平分∠ABC，∠A=120°，BD=
如图，等腰梯形ABCD中，AD∥BC，AB=CD，对角线BD平分∠ABC，且BD⊥DC，上底AD=3cm．
如图，等腰梯形ABCD中，AD∥BC，AB=CD，BD平分∠ABC，BD⊥DC，延长BC到E，使CE=AD．