题目内容
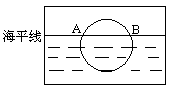
如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A、B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为10分钟,则“图上”太阳升起的平均速度为( )
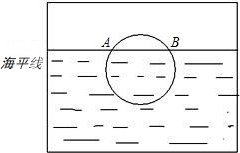

| A、0.5厘米/分 | B、0.8厘米/分 | C、1.0厘米/分 | D、1.6厘米/分 |
分析:设圆心为O,过O作AB的垂线,设垂足为C,延长CO交⊙O于D,根据垂径定理及勾股定理求出CD的长即可.
解答: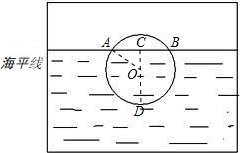 解:如图;过圆心O作OC⊥AB于C,延长CO交⊙O于D,连接OA;
解:如图;过圆心O作OC⊥AB于C,延长CO交⊙O于D,连接OA;
Rt△OAC中,AC=
AB=4cm,OA=5cm;
根据勾股定理,得:OC=
=3cm;
∴CD=OC+OD=8cm;
所以太阳上升的速度为:8÷10=0.8厘米/分;故选B.
 解:如图;过圆心O作OC⊥AB于C,延长CO交⊙O于D,连接OA;
解:如图;过圆心O作OC⊥AB于C,延长CO交⊙O于D,连接OA;Rt△OAC中,AC=
| 1 |
| 2 |
根据勾股定理,得:OC=
| OA2-AC2 |
∴CD=OC+OD=8cm;
所以太阳上升的速度为:8÷10=0.8厘米/分;故选B.
点评:此题主要考查了垂径定理及勾股定理的应用.能够弄清太阳10分钟内所走的路程是解答此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
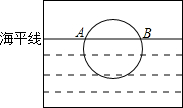 如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A、B两点,他测得“图上”圆的半径为10厘米,AB=16厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为10分钟,则“图上”太阳升起的速度为( )
如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A、B两点,他测得“图上”圆的半径为10厘米,AB=16厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为10分钟,则“图上”太阳升起的速度为( )| A、0.4厘米/分 | B、0.6厘米/分 | C、1.0厘米/分 | D、1.6厘米/分 |
 9、每位同学都能感受到日出时美丽的景色.如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,则“图上”太阳升起的速度为( )
9、每位同学都能感受到日出时美丽的景色.如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,则“图上”太阳升起的速度为( )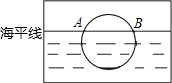 如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A、B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为10分钟,则“图上”太阳升起的平均速度为
如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A、B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为10分钟,则“图上”太阳升起的平均速度为