题目内容
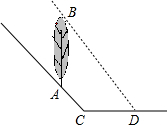当太阳光线与地面成60°角时，在坡度为i=1：2的斜坡上的一棵树AB落在坡面上的影子AC长为5米，落在水平线上的影子CD长为3米，求这棵树的高度．
分析：首先把实际问题转化为直角三角形问题，延长DC和BA交于点E，先由直角三角形ACE及已知坡度为i=1：2的斜坡求出AE和CE，再由直角△BED求出BE，从而求出这棵树AB的高度．
解答：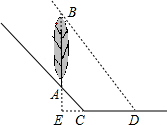
解：延长DC和BA交于点E，
设AE=x，则由坡度为i=1：2的斜坡得，CE=2x，
∴x2+（2x）2=52，
由实际问题解得：
x=
，
∴AE=
，CE=2
，
则ED=3+2
，
∴BE=ED•tan60°=（3+2
）×
=3
+2
，
∴AB=BE-AE=3
+2
-
．
解：延长DC和BA交于点E，设AE=x，则由坡度为i=1：2的斜坡得，CE=2x，
∴x2+（2x）2=52，
由实际问题解得：
x=
| 5 |
∴AE=
| 5 |
| 5 |
则ED=3+2
| 5 |
∴BE=ED•tan60°=（3+2
| 5 |
| 3 |
| 3 |
| 15 |
∴AB=BE-AE=3
| 3 |
| 15 |
| 5 |
点评：此题考查的知识点是解直角三角形的应用，关键是把实际问题转化为直角三角形问题，通过两个直角三角形求解．
练习册系列答案
相关题目
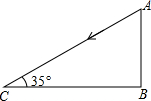某课外活动小组测量学校旗杆的高度，当太阳光线与地面成35°角时，渢旗杆AB在地面上的投影BC的长为20米（如图）．求旗杆AB的高度．（sin35°≈0.6，cos35°≈0.8，tan35°≈0.7）
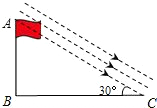课外活动小组测量学校旗杆的高度，如图，当太阳光线与地面成30°角时，测得旗杆AB在地面上的投影BC长为24米，则旗杆AB的高度约是
如图，当太阳光线与地面成30°时，测得旗杆AB在地面上的影子BC长为15米，那么旗杆AB的高度是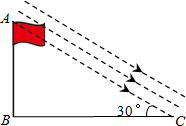
课外活动小组测量学校旗杆的高度．如图，当太阳光线与地面成30°角时，测得旗杆AB在地面上的投影BC长为24米，则旗杆AB的高度约是