题目内容
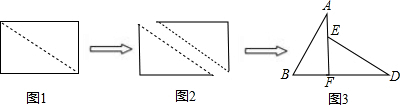
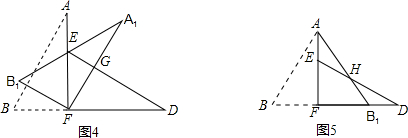
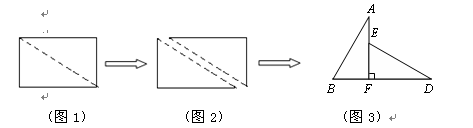
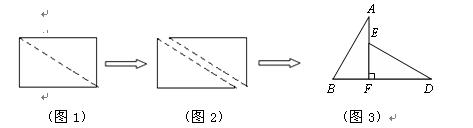
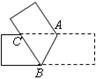
如图，将一张直角三角形纸片ABC（∠ACB=90°）沿线段CD折叠使B落在B1处，若∠B1CB=150°，则∠ACD的度数是
- A.10°
- B.15°
- C.25°
- D.75°
B
分析：根据翻折的性质可知：∠BCD=∠B1CD，又∠BCD+∠B1CD=∠B1CB=150°，继而即可求出∠BCD的值，又∠ACD+∠BCD=∠ACB=90°，继而即可求出∠ACD的度数．
解答：∵△B1CD时由△BCD翻折得到的，
∴∠BCD=∠B1CD，
又∠BCD+∠B1CD=∠B1CB=150°，
∴∠BCD=75°，
又∠ACD+∠BCD=∠ACB=90°，
∴∠ACD=15°．
故选B．
点评：本题考查翻折变换的知识，难度适中，解题关键是掌握折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
分析：根据翻折的性质可知：∠BCD=∠B1CD，又∠BCD+∠B1CD=∠B1CB=150°，继而即可求出∠BCD的值，又∠ACD+∠BCD=∠ACB=90°，继而即可求出∠ACD的度数．
解答：∵△B1CD时由△BCD翻折得到的，
∴∠BCD=∠B1CD，
又∠BCD+∠B1CD=∠B1CB=150°，
∴∠BCD=75°，
又∠ACD+∠BCD=∠ACB=90°，
∴∠ACD=15°．
故选B．
点评：本题考查翻折变换的知识，难度适中，解题关键是掌握折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
阅读快车系列答案
相关题目
