题目内容
下列命题:
①在实数范围内,一元二次方程ax2+bx+c=0(a≠0)的根为x= ;
;
②若a+b+c=0,则b2-4ac≥0;
③△ABC的三边为a,b,c是关于x的一元二次方程(c+b)x2-2ax+c-b=0有两个相等的实数根,则△ABC为直角三角形;
④关于x的方程(k-3)x2+kx+1=0总有实数根.其中正确的是
- A.①②③④
- B.只有①③④
- C.只有②③
- D.只有②③④
D
分析:根据一元二次方程的求根根式对①进行判断;由于x=1时,a+b+c=0,而a≠0,说明一元二次方程有实数根,根据△的意义可对②进行判断;根据△的意义得到△=(2a)2-4(c+b)(c-b)=0,变形得a2+b2=c2,然后根据勾股定理的逆定理对③进行判断;讨论:当k-3=0,即k=3,方程为3x+1=0,方程有一个实数解,当k-3≠0,△=k2-4(k-3)=(k-2)2+8>0,方程有方程有两个不相等实数根,于是可对④进行判断.
解答:在实数范围内,一元二次方程ax2+bx+c=0(a≠0)的根为x= (b2-4ac≥0),所以①错误;若a+b+c=0,则x=1,方程有实数解,而a≠0,方程有实数根,所以②正确;△=(2a)2-4(c+b)(c-b)=0,则a2+b2=c2,△ABC为直角三角形,所以③正确;当k-3=0,即k=3,方程为3x+1=0,x=-
(b2-4ac≥0),所以①错误;若a+b+c=0,则x=1,方程有实数解,而a≠0,方程有实数根,所以②正确;△=(2a)2-4(c+b)(c-b)=0,则a2+b2=c2,△ABC为直角三角形,所以③正确;当k-3=0,即k=3,方程为3x+1=0,x=- ,当k-3≠0,△=k2-4(k-3)=(k-2)2+8>0,方程有两个不相等实数根,所以方程(k-3)x2+kx+1=0总有实数根,所以④正确.
,当k-3≠0,△=k2-4(k-3)=(k-2)2+8>0,方程有两个不相等实数根,所以方程(k-3)x2+kx+1=0总有实数根,所以④正确.
故选D.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了勾股定理的逆定理.
分析:根据一元二次方程的求根根式对①进行判断;由于x=1时,a+b+c=0,而a≠0,说明一元二次方程有实数根,根据△的意义可对②进行判断;根据△的意义得到△=(2a)2-4(c+b)(c-b)=0,变形得a2+b2=c2,然后根据勾股定理的逆定理对③进行判断;讨论:当k-3=0,即k=3,方程为3x+1=0,方程有一个实数解,当k-3≠0,△=k2-4(k-3)=(k-2)2+8>0,方程有方程有两个不相等实数根,于是可对④进行判断.
解答:在实数范围内,一元二次方程ax2+bx+c=0(a≠0)的根为x=
 (b2-4ac≥0),所以①错误;若a+b+c=0,则x=1,方程有实数解,而a≠0,方程有实数根,所以②正确;△=(2a)2-4(c+b)(c-b)=0,则a2+b2=c2,△ABC为直角三角形,所以③正确;当k-3=0,即k=3,方程为3x+1=0,x=-
(b2-4ac≥0),所以①错误;若a+b+c=0,则x=1,方程有实数解,而a≠0,方程有实数根,所以②正确;△=(2a)2-4(c+b)(c-b)=0,则a2+b2=c2,△ABC为直角三角形,所以③正确;当k-3=0,即k=3,方程为3x+1=0,x=- ,当k-3≠0,△=k2-4(k-3)=(k-2)2+8>0,方程有两个不相等实数根,所以方程(k-3)x2+kx+1=0总有实数根,所以④正确.
,当k-3≠0,△=k2-4(k-3)=(k-2)2+8>0,方程有两个不相等实数根,所以方程(k-3)x2+kx+1=0总有实数根,所以④正确.故选D.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了勾股定理的逆定理.

练习册系列答案
相关题目
下列四个数在实数范围内没有平方根的是( )
| A、-(-1) | ||
| B、0 | ||
| C、-32 | ||
D、
|
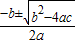 ;
;