Question

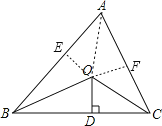
【题目】如图，在△ABC中，点O是∠ABC、∠ACB平分线的交点，AB＋BC＋AC＝20，过O作OD⊥BC于D点，且OD＝3，求△ABC的面积．

Answer 1

【答案】30

【解析】

试题作OE⊥AB于E，OF⊥AC于F，连结OA，如图，根据角平分线的性质得OE=OF=OD=3，然后根据三角形面积公式和S△ABC=S△ABO+S△BCO+S△ACO进行计算即可．

试题解析：作OE⊥AB于E，OF⊥AC于F，连结OA，如图，

∵点O是∠ABC、∠ACB角平分线的交点，
∴OE=OD，OF=OD，
即OE=OF=OD=3，
∴S△ABC=S△ABO+S△BCO+S△ACO=ABOE+BCOD+ACOF
=×3×（AB+BC+AC）
=×3×20
=30．