题目内容
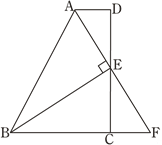
【题目】如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连接AD,AC,BC,BD,若AD=AC=AB,则下列结论:①AE垂直平分CD,②AC平分∠BAD,③△ABD是等边三角形,④∠BCD的度数为150°,其中正确的个数是( )

A.1B.2C.3D.4
【答案】D
【解析】
首先证明△AEC≌△BED,得到AC=BD=AB=AD,得到△ABD是等边三角形,③正确;根据 ABE与 CDE都是等腰直角三角形,得到∠CAB=∠CAD=30°∠CAE=∠EAD=15°得到①②正确; ABC,CAD为等腰三角形,顶角都为30°,得到∠ACB=∠ABC=75°,∠ACD=∠ADC=75°,得出∠BCD的度数为150°④正确
解:∵ ABE与 CDE都是等腰直角三角形
∴AE=BE, DE=CE
∵∠AEB=∠DEC=90°
∴∠AEC=∠DEB
∴△AEC≌△BED
∴AC=BD
∵AD=AC=AB
∴AD=BD=AB
∴② ABD是等边三角形正确
∴∠ABD=∠BAD=∠ADB=60°
∵ ABE与 CDE都是等腰直角三角形
∴∠EAB=∠ABE=45°
∴∠CAB=30°,∠CAE=∠EAD=15°
∴AE为∠CAD的角平分线
∵ ABD为等腰三角形
∴①AE垂直平分CD正确
∴∠CAD=30°
∴②AC平分∠BAD正确
∵ ABC为等腰三角形,顶角∠BAC=30°
∴∠ACB=∠ABC=75°
同理∠ACD=∠ADC=75°
∴④∠BCD的度数为150°正确.
故选D

【题目】夷陵区园林处为了对一段公路进行绿化,计划购买A、B两种风景树,已知若用8000元买A种树要比买B种树多买20棵,A、B两种树的相关信息如下表:
项目品种 | 单价(元/棵) | 成活率 |
A | m | 91% |
B | 100 | 97% |
(1)求表中m的值;
(2)预计对这段公路的绿化需购1000棵这样的风景树.若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?最低费用为多少?