Question

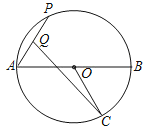
【题目】如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC.

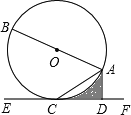
（1）求证：EF是⊙O的切线；

（2）求证：AC2=AD·AB；

（3）若⊙O的半径为2，∠ACD=300，求图中阴影部分的面积．

Answer 1

【答案】解：（1）证明：连接OC，

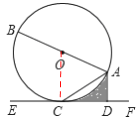
∵OA=OC，∴∠BAC=∠OCA。

∵∠DAC=∠BAC，∴∠OCA=∠DAC。∴OC∥AD。

∵AD⊥EF，∴OC⊥EF。

∵OC为半径，∴EF是⊙O的切线。

（2）证明：∵AB为⊙O直径，AD⊥EF，

∴∠BCA=∠ADC=90°。

∵∠DAC=∠BAC，∴△ACB∽△ADC。

∴。∴AC2=ADAB。

（3）∵∠ACD=30°，∠OCD=90°，∴∠OCA=60°.

∵OC=OA，∴△OAC是等边三角形。∴AC=OA=OC=2，∠AOC=60°。

∵在Rt△ACD中，AD=AC=1。

由勾股定理得：DC=，

∴阴影部分的面积是S=S梯形OCDA﹣S扇形OCA=×（2+1）×﹣。

【解析】

试题（1）连接OC，根据OA=OC推出∠BAC=∠OCA=∠DAC，推出OC∥AD，得出OC⊥EF，根据切线的判定推出即可。

（2）证△ADC∽△ACB，得出比例式，即可推出答案。

（3）求出等边三角形OAC，求出AC、∠AOC，在Rt△ACD中，求出AD、CD，求出梯形OCDA和扇形OCA的面积，相减即可得出答案。