题目内容
如图所示,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,如图①,然后将△ADE绕A点顺时针旋转一定角度,得到图②,然后将BD、CE分别延长至M、N,使DM= BD,EN=
BD,EN= CE,得到图③,请解答下列问题:
CE,得到图③,请解答下列问题:
(1)若AB=AC,请探究下列数量关系:
①在图②中,BD与CE的数量关系是________________;
②在图③中,猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系,并证明你的猜想;
(2)若AB=k·AC(k>1),按上述操作方法,得到图④,请继续探究:AM与AN的数量关系、∠MAN与∠BAC的数量关系,直接写出你的猜想,不必证明.
 BD,EN=
BD,EN= CE,得到图③,请解答下列问题:
CE,得到图③,请解答下列问题:(1)若AB=AC,请探究下列数量关系:
①在图②中,BD与CE的数量关系是________________;
②在图③中,猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系,并证明你的猜想;
(2)若AB=k·AC(k>1),按上述操作方法,得到图④,请继续探究:AM与AN的数量关系、∠MAN与∠BAC的数量关系,直接写出你的猜想,不必证明.

(1)①BD=CE;
②AM=AN,∠MAN=∠BAC 理由如下:
∵在图①中,DE//BC,AB=AC
∴AD="AE."
在△ABD与△ACE中 ∴△ABD≌△ACE.
∴△ABD≌△ACE.
∴BD=CE,∠ACE=∠ABD.
在△DAM与△EAN中,
∵DM= BD,EN=
BD,EN= CE,BD=CE,∴DM=EN,∵∠AEN=∠ACE+∠CAE,∠ADM=∠ABD+∠BAD,∴∠AEN=∠ADM.
CE,BD=CE,∴DM=EN,∵∠AEN=∠ACE+∠CAE,∠ADM=∠ABD+∠BAD,∴∠AEN=∠ADM.
又∵AE=AD,∴△ADM≌△AEN.∴AM=AN,∠DAM=∠EAN.∴∠MAN=∠DAE=∠BAC.
∴AM=AN,∠MAN=∠BAC.
(2)AM=kAN,∠MAN=∠BAC.
②AM=AN,∠MAN=∠BAC 理由如下:
∵在图①中,DE//BC,AB=AC
∴AD="AE."
在△ABD与△ACE中
 ∴△ABD≌△ACE.
∴△ABD≌△ACE. ∴BD=CE,∠ACE=∠ABD.
在△DAM与△EAN中,
∵DM=
 BD,EN=
BD,EN= CE,BD=CE,∴DM=EN,∵∠AEN=∠ACE+∠CAE,∠ADM=∠ABD+∠BAD,∴∠AEN=∠ADM.
CE,BD=CE,∴DM=EN,∵∠AEN=∠ACE+∠CAE,∠ADM=∠ABD+∠BAD,∴∠AEN=∠ADM. 又∵AE=AD,∴△ADM≌△AEN.∴AM=AN,∠DAM=∠EAN.∴∠MAN=∠DAE=∠BAC.
∴AM=AN,∠MAN=∠BAC.
(2)AM=kAN,∠MAN=∠BAC.
(1)①根据题意和旋转的性质可知△AEC≌△ADB,所以BD=CE;
②根据题意可知∠CAE=BAD,AB=AC,AD=AE,所以得到△BAD≌△CAE,在△ABM和△ACN中,
DM=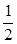 BD,EN=
BD,EN=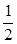 CE,可证△ABM≌△ACN,所以AM=AN,即∠MAN=∠BAC.
CE,可证△ABM≌△ACN,所以AM=AN,即∠MAN=∠BAC.
(2)直接类比(1)中结果可知AM=k•AN,∠MAN=∠BAC.
②根据题意可知∠CAE=BAD,AB=AC,AD=AE,所以得到△BAD≌△CAE,在△ABM和△ACN中,
DM=
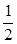 BD,EN=
BD,EN=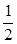 CE,可证△ABM≌△ACN,所以AM=AN,即∠MAN=∠BAC.
CE,可证△ABM≌△ACN,所以AM=AN,即∠MAN=∠BAC.(2)直接类比(1)中结果可知AM=k•AN,∠MAN=∠BAC.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 与
与 ,旋转长方形
,旋转长方形

 绕点
绕点 逆时针旋转
逆时针旋转 ,得到
,得到 .若点
.若点 的坐标为
的坐标为 ,则点
,则点 的坐标为 .
的坐标为 .


 (
( ,且
,且