题目内容
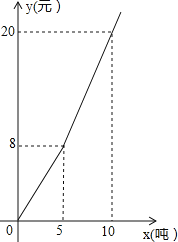
【题目】某市草莓种植大户，需将一批草莓运往省内某地，运输可选用A、B两种运输方式的一种，都可在同一地点将这批草莓上车沿同一条公路运往目的地，在运输过程中的有关数据如下：
项目 运输方式 | 装卸时间（小时） | 装卸费用（元） | 途中平均速度（千米/时） | 途中平均运费（元/千米） |
A | 2 | 1100 | 80 | 8 |
B | 3 | 1500 | 100 | 7 |
若这批草莓在运输过程（包括装卸时间）中，损耗为160元/时，设运输路程为
（
）千米，A种运输方式所需总费用为
元，B种运输方式所需总费用为
元.（总费用=运输过程损耗费用+运费+装卸费用）
（1）分别求出、与的关系式；
（2）应采用哪种运输方式，才使运输所需总费用最小？
【答案】（1）yA=10x+1420；yB=8.6x+1980；（2）当运输路程为400千米时选哪个都行；当运输路程大于400千米时选B更合适；当运输路程小于400千米时选A更合适．
【解析】
（1）可根据总运费=（装卸的时间+行驶的时间）×草莓的损耗+行驶的费用+装卸的费用．来列出A，B的总运费和运输路程的关系式；
（2）可将（1）中得出的式子进行比较，得出最省钱的方案．
（1）由题意得：
yA=（2+
）×160+8x+1100=10x+1420
yB=（3+
）×160+7x+1500=8.6x+1980；
（2）①当yA=yB时，10x+1420=8.6x+1980，x=400，当运输路程为400千米时选哪个都行．
②当yA＞yB时，10x+1420＞8.6x+1980，x＞400，当运输路程大于400千米时选B更合适．
③当yA＜yB时，10x+1420＜8.6x+1980，x＜400，当运输路程小于400千米时选A更合适．
名师指导期末冲刺卷系列答案
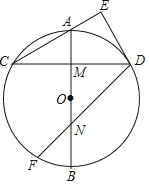
开心蛙口算题卡系列答案
【题目】如图1，Rt△ABC中，∠ACB＝90°，点D为AB边上的动点（点D不与点A，点B重合），过点D作ED⊥CD交直线AC于点E，已知∠A＝30°，AB＝4cm，在点D由点A到点B运动的过程中，设AD＝xcm，AE＝ycm．
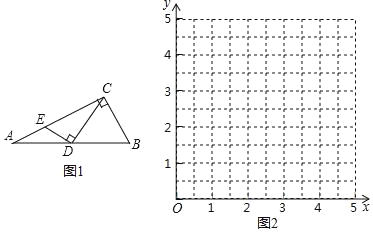
小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x/cm | … |
| 1 |
| 2 |
| 3 |
| … |
y/cm | … | 0.4 | 0.8 | 1.0 |
| 1.0 | 0 | 4.0 | … |
（说明：补全表格时相关数值保留一位小数）
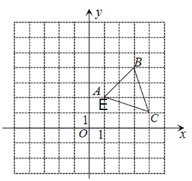
（2）在如图2的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：当AE＝
AD时，AD的长度约为 cm．
