Question

【题目】如图，已知AB为⊙O的直径，AD、BD是⊙O的弦，BC是⊙O的切线，切点为B，OC∥AD，BA、CD的延长线相交于点E．

（1）求证：DC是⊙O的切线；

（2）若AE=1，ED=3，求⊙O的半径．

Answer 1

【答案】（1）证明见解析；（2）4．

【解析】试题分析：(1)、连接DO，根据平行线的性质得出∠DAO=∠COB，∠ADO=∠COD，结合OA=OD得出∠COD=∠COB，从而得出△COD和△COB全等，从而得出切线；(2)、设⊙O的半径为R，则OD=R，OE=R+1，根据Rt△ODE的勾股定理求出R的值得出答案．

试题解析：（1）证明：连结DO． ∵AD∥OC， ∴∠DAO=∠COB，∠ADO=∠COD．

又∵OA=OD， ∴∠DAO=∠ADO， ∴∠COD=∠COB．

在△COD和△COB中 ∵OD=OB，OC=OC， ∴△COD≌△COB（SAS），

∴∠CDO=∠CBO． ∵BC是⊙O的切线， ∴∠CBO=90°， ∴∠CDO=90°，

又∵点D在⊙O上， ∴CD是⊙O的切线；

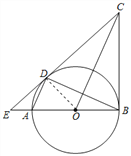
（2）设⊙O的半径为R，则OD=R，OE=R+1， ∵CD是⊙O的切线， ∴∠EDO=90°，

∴ED2+OD2=OE2， ∴32+R2=（R+1）2， 解得R=4， ∴⊙O的半径为4．