题目内容
如图，有一个等腰三角形ABD，AB=AD．
（1）请你用尺规作图法作出点A关于轴BD的对称点C；（不用写作法，但保留作图痕迹）
（2）连接（1）中的BC和CD，请判断四边形ABCD的形状，并证明你的结论．
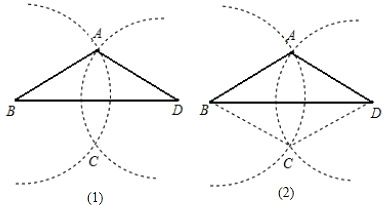解：（1）如图，（2）∵C点是点A关于轴BD的对称点，
∴AB=AD=BC=CD，
∴四边形ABCD是菱形．
分析：（1）分别以BD为圆心，以AB或AD为半径画弧即可作出点A关于轴BD的对称点C；
（2）根据菱形的判定定理：对角线互相垂直平分或四边相等即可判定四边形ABCD的形状．
点评：菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义；②四边相等；③对角线互相垂直平分．此题根据③或②都可以判定四边形的形状．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
互唯一确定的．
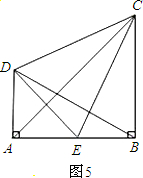
教材中第25章锐角的三角比，在这章的小结中有如下一段话：锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.
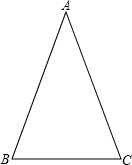
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时
sad A=
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义，解下列问题：
（1）sad
的值为（ ▼ ）
（2）对于
，∠A的正对值sad A的取值范围是 ▼ .
（3）已知
，其中
为锐角，试求sad的值.
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时
sad A=
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义，解下列问题：
（1）sad
的值为（ ▼ ）A． | B．1 | C． | D．2 |
，∠A的正对值sad A的取值范围是 ▼ .（3）已知
，其中为锐角，试求sad的值. 教材中第25章锐角的三角比，在这章的小结中有如下一段话：锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时
sad A=
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义，解下列问题：
（1）sad 
的值为（ ▼ ）
A． | B．1 | C． | D．2 |
，∠A的正对值sad A的取值范围是 ▼ .（3）已知
，其中
为锐角，试求sad的值. 
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
的值为（ ▼ ）
B.
1 C. 
D.
2
，∠A的正对值sad A的取值范围是 ▼ .
，其中
为锐角，试求sad