题目内容
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点.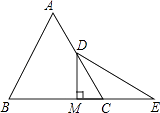
【答案】证明:连接BD,
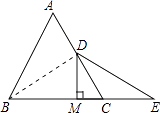
∵在等边△ABC,且D是AC的中点,
∴∠DBC= ![]() ∠ABC=
∠ABC= ![]() ×60°=30°,∠ACB=60°,
×60°=30°,∠ACB=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E,
∴∠E=30°,
∴∠DBC=∠E=30°,
∴BD=ED,△BDE为等腰三角形,
又∵DM⊥BC,
∴M是BE的中点.
【解析】要证M是BE的中点,根据题意可知,证明△BDE△为等腰三角形,利用等腰三角形三线合一的性质即可得证。
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目