题目内容
【题目】如图,AB是半圆O的直径,C.E在半圆O上,CD⊥AB于点D,且CD=![]() .
.
(1)如图1.若点C是![]() 的中点,求AE的长;
的中点,求AE的长;
(2)如图2,若∠B=30°,连接CE,点P为CE中点,连接DP,交AE于点F,记以C为圆心,CP为半径的圆为⊙C.探究AE与⊙C的位置关系,并说明理由.
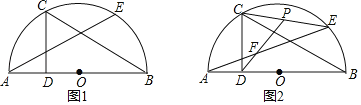
【答案】(1)AE=2![]() ;(2)AE与⊙C相切,理由见解析.
;(2)AE与⊙C相切,理由见解析.
【解析】
(1)连接OC,交AE于点F,由点C是![]() 的中点,根据垂径定理可得,得OC⊥AE,
的中点,根据垂径定理可得,得OC⊥AE,![]() ,依据AAS证明△AFO≌△CDO,即可求得AE的长;
,依据AAS证明△AFO≌△CDO,即可求得AE的长;
(2)根据点P为CE中点,得CP=![]() CE,由同弧所对圆周角相等得∠E=∠B=30°,作CG⊥AE于G,依据含有30度的直角三角形的性质得到CG=
CE,由同弧所对圆周角相等得∠E=∠B=30°,作CG⊥AE于G,依据含有30度的直角三角形的性质得到CG=![]() CE,从而CP=CG,即可证明AE与⊙C相切.
CE,从而CP=CG,即可证明AE与⊙C相切.
解:(1)如图1,
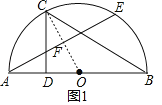
连接OC,交AE于点F,
![]() 点C是
点C是![]() 的中点,
的中点,![]() ,2
,2![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
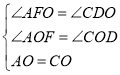
![]() ≌
≌![]() ,
,![]() ,
,![]() ;
;
(2)AE与⊙C相切,理由如下:
如图2,作CG⊥AE于G,则![]() ,
,
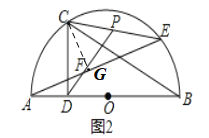
∵点P为CE中点,
![]() ,
,
∵![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴CG=CP,
∴以C为圆心,CP为半径的圆为⊙C与AE相切.
所以AE与⊙C相切.

练习册系列答案
相关题目