题目内容
若函数y=ax和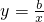
的图象无公共点，且ab≠0，则可断定
- A.a＞0，b＞0
- B.a＜0，b＞0
- C.a＜0，b＞0
- D.ab＜0
D
分析：由函数y=ax的图象规律可知．
解答：∵ab≠0，
∴a≠0，b≠0．
又因为两个图象无公共点，
所以a＞0时，b＜0，
而当a＜0时，则b＞0，
所以可得ab＜0．
故选D．
点评：此题运用了一次函数和反比例函数的图象特点，是数形结合的思想．
规律：当a＞0，则函数y=ax的图象经过一、三象限和原点，当a＜0时，则函数y=ax的图象经过二、四象限和原点．当b＞0时，反比例函数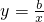的图象在一、三象限，当b＜0时，反比例函数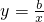的图象在二、四象限．
分析：由函数y=ax的图象规律可知．
解答：∵ab≠0，
∴a≠0，b≠0．
又因为两个图象无公共点，
所以a＞0时，b＜0，
而当a＜0时，则b＞0，
所以可得ab＜0．
故选D．
点评：此题运用了一次函数和反比例函数的图象特点，是数形结合的思想．
规律：当a＞0，则函数y=ax的图象经过一、三象限和原点，当a＜0时，则函数y=ax的图象经过二、四象限和原点．当b＞0时，反比例函数
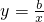的图象在一、三象限，当b＜0时，反比例函数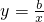的图象在二、四象限． 
练习册系列答案
相关题目
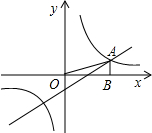如图，反比例函数
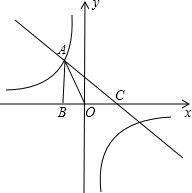于点B，且△AOB的面积为
在平面直角坐标系xOy中，若一次函数y=ax+b的图象与反比例函数y=
的图象无公共点，且ab≠0，则可断定（ ）