题目内容
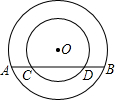如图，在以O为圆心的两个同心圆的圆中，大圆的弦AB交小圆于C、D两点，试判断AC与BD的大小关系，并说明理由．
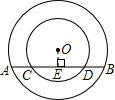解：如图：过O作OE⊥AB，则OE平分AB，同理OE平分CD，
则有AE=BE，CE=DE，
则有AE-CE=BE-DE，
即AC=BD．
分析：过圆心O作弦的垂线OE，根据垂径定理，OE平分AB和CD，可以说明AC=BD．
点评：本题考查的是垂径定理，根据题意过圆心作弦的垂线，由垂径定理有：AE=BE，CE=DE，然后把这两个等式相减得到AC=BD．
练习册系列答案
名校课堂系列答案
相关题目
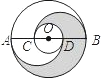如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC=CD=DB，分别以C、D为圆心，以CD为半径作圆．若AB=6cm，则图中阴影部分的面积为
9、如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，已知AB=8，大圆半径为5，则小圆半径为（ ）
（2006•静安区二模）如图，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于B，大圆的弦BC⊥AB，过点C作大圆的切线交AB的延长线于D，OC交小圆于E
如图，在以O为圆心的两个同心圆中，MN为大圆的直径，交小圆于点P、Q，大圆的弦MC交小圆于点A、B．若OM=2，OP=1，MA=AB=BC，则△MBQ的面积为
如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆的半径为5cm，小圆的半径为3cm，则弦AB的长为（ ）