题目内容
一段公路路面的坡度为i=1：2.4．如果某人沿着这段公路向上行走了260m，那么此人升高了
- A.50m
- B.100m
- C.150m
- D.200m
B
分析：已知了坡面长为260米，可根据坡度比设出两条直角边的长度，根据勾股定理可列方程求出坡面的铅直高度，即此人上升的最大高度．
解答：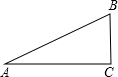
解：如图，Rt△ABC中，tanA=
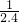，AB=260米．
设BC=x，则AC=2.4x，根据勾股定理，得：
x2+（2.4x）2=2602，
解得x=100（负值舍去）．
故选B．
点评：此题主要考查学生对坡度坡角的掌握及勾股定理、三角函数的运用能力，难度不大，注意掌握坡度的定义及数形结合思想的应用．
分析：已知了坡面长为260米，可根据坡度比设出两条直角边的长度，根据勾股定理可列方程求出坡面的铅直高度，即此人上升的最大高度．
解答：
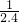解：如图，Rt△ABC中，tanA=，AB=260米．设BC=x，则AC=2.4x，根据勾股定理，得：
x2+（2.4x）2=2602，
解得x=100（负值舍去）．
故选B．
点评：此题主要考查学生对坡度坡角的掌握及勾股定理、三角函数的运用能力，难度不大，注意掌握坡度的定义及数形结合思想的应用．
练习册系列答案
相关题目
一段公路的坡度为1：3，某人沿这段公路路面前进100米，那么他上升的最大高度是（ ）
| A、30米 | ||
| B、10米 | ||
C、3
| ||
D、10
|
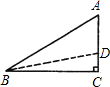某山区计划修建一条通过小山的公路，经测量，从山底B到山顶A的坡角是30°，斜坡AB长为100米，根据地形，要求修好的公路路面BD的坡度为1：5（假定A，D处于同一垂直线上），为了减少工程量，若AD≤20米，则直接开挖修建公路；若AD＞20米，就要重新设计．那么你认为这段公路是否需要重新设计？答：
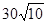米 D. 
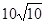米