��Ŀ����
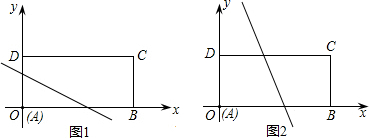
��ƽ��ֱ������ϵ�У���֪����ABCD�У���AB=2����AD=1����AB��AD�ֱ���x�ᡢy����������ϣ���A������ԭ���غϣ��������۵���ʹ��A���ڱ�DC�ϣ����A���ǵ�A���ڱ�DC�ϵĶ�Ӧ�㣮��1��������ABCD��ֱ��y=-
| 1 | 2 |
��2��������ABCD��ֱ��y=kx+b�۵�ʱ��
�����A������꣨��k��ʾ�������k��b֮��Ĺ�ϵʽ��
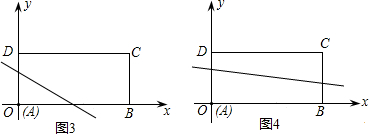
��������ǰ��ۺ����ڵ�ֱ������ε�λ�÷�Ϊ��ͼ2��3��4��ʾ���������Σ�����ֱ�д��ÿ������ʱk��ȡֵ��Χ��������ֱ������ÿ�������µĺ����ϣ�k��ȡֵ��Χ��
��������1����ֱ��y=-
x+b��CD���ڵ�E����OB���ڵ�F������A��O����OE=b��OF=2b�����A�������Ϊ��a��1�������ݡ�DOA��ס�OFE������
=
����
=
������a=
���ɵõ�A�������Ϊ��
��1��������A��E����A��E=OE=b�����ݹ��ɶ�����A��E2=A��D2+DE2����b2=��
��2+��1-b��2�����b=
��
��2����ֱ��y=kx+b��OD���ڵ�E����OB���ڵ�F������A��O����OE=b��OF=-
�����A�������Ϊ��a��1����֤��DOA��ס�OFE������
=
����
=
������a=-k��A��������Ϊ��-k��1��������A��E����Rt��DEA���У�DA��=-k��DE=1-b��A��E=b������A��E2=A��D2+DE2����b2=��-k��2+��1-b��2������b=
��
��3������ͼ��;��εı߳���ֱ�ӵó�k��ȡֵ��Χ��������ͼ2�У�-2��k��-1��ͼ3�У�-1��k��-2+
��ͼ4�У�-2+
��k��0��
| 1 |
| 2 |
| DA�� |
| OE |
| DO |
| OF |
| a |
| b |
| 1 |
| 2b |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 8 |
��2����ֱ��y=kx+b��OD���ڵ�E����OB���ڵ�F������A��O����OE=b��OF=-
| b |
| k |
| DA�� |
| OE |
| DO |
| OF |
| a |
| b |
| 1 | ||
-
|
| k2+1 |
| 2 |
��3������ͼ��;��εı߳���ֱ�ӵó�k��ȡֵ��Χ��������ͼ2�У�-2��k��-1��ͼ3�У�-1��k��-2+
| 3 |
| 3 |
��� �⣺��1����ͼ1����ֱ��y=-
�⣺��1����ͼ1����ֱ��y=-
x+b��CD���ڵ�E����OB���ڵ�F����y�ύ��G�㣬����A'O����OE=b��OF=2b�����A�������Ϊ��a��1����
�ߡ�DOA��+��A��OF=90�㣬��OFE+��A��OF=90�㣬
���DOA��=��OFE��
���DOA��ס�OFE��
��
=
����
=
��
��a=
��
���A���������
��1����
����A��E����A��E=OE=b��
��Rt��DEA���У����ݹ��ɶ�����A��E2=A��D2+DE2��
��b2=��
��2+��1-b��2��
���b=
��
��2����ͼ1����ֱ��y=kx+b��OD���ڵ�E����OB���ڵ�F������A'O����
OE=b��OF=-
��
���A���������a��1����
�ߡ�DOA��+��A��OF=90�㣬��OFE+��A'OF=90�ȣ�
���DOA��=��OFE��
���DOA��ס�OFE��
��
=
����
=
��
��a=-k��
��A��������Ϊ��-k��1������7�֣�
����A��E����Rt��DEA����DA��=-k��DE=1-b��A��E=b��
��A��E2=A��D2+DE2��
��b2=��-k��2+��1-b��2��
��b=
��
��3��������ͼ2�У�-2��k��-1��
ͼ3�У�-1��k��-2+
��
ͼ4�У�-2+
��k��0��
 �⣺��1����ͼ1����ֱ��y=-
�⣺��1����ͼ1����ֱ��y=-| 1 |
| 2 |
�ߡ�DOA��+��A��OF=90�㣬��OFE+��A��OF=90�㣬
���DOA��=��OFE��
���DOA��ס�OFE��
��
| DA�� |
| OE |
| OD |
| OF |
| a |
| b |
| 1 |
| 2b |
��a=
| 1 |
| 2 |
���A���������
| 1 |
| 2 |
����A��E����A��E=OE=b��
��Rt��DEA���У����ݹ��ɶ�����A��E2=A��D2+DE2��
��b2=��
| 1 |
| 2 |
���b=
| 5 |
| 8 |
��2����ͼ1����ֱ��y=kx+b��OD���ڵ�E����OB���ڵ�F������A'O����
OE=b��OF=-
| b |
| k |
���A���������a��1����
�ߡ�DOA��+��A��OF=90�㣬��OFE+��A'OF=90�ȣ�
���DOA��=��OFE��
���DOA��ס�OFE��
��
| DA�� |
| OE |
| DO |
| OF |
| a |
| b |
| 1 | ||
-
|
��a=-k��
��A��������Ϊ��-k��1������7�֣�
����A��E����Rt��DEA����DA��=-k��DE=1-b��A��E=b��
��A��E2=A��D2+DE2��
��b2=��-k��2+��1-b��2��
��b=
| k2+1 |
| 2 |
��3��������ͼ2�У�-2��k��-1��
ͼ3�У�-1��k��-2+
| 3 |
ͼ4�У�-2+
| 3 |
����������һ���й��۵������⣬��Ҫ����һ�κ������ı��Ρ������ε�֪ʶ�������йᴩ�˷���˼������ν�ϵ�˼�룬��ע����ᣮ

��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
�����Ŀ
 ����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB=
����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB= 18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任��
18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任��