题目内容
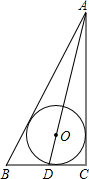如图，⊙O为△ABC的内切圆，∠C=90度，OA的延长线交BC于点D，AC=4，CD=1，则⊙O的半径等于
- A.
- B.
- C.
- D.
A
分析：设圆O与AC的切点为M，圆的半径为r，求得△AOM∽△ADC，利用相似比作为相等关系可列式：1=（4-r）：4，解之即可．
解答：
解：设圆O与AC的切点为M，圆的半径为r，
如图，连接OM，
∵∠C=90°
∴CM=r，
∵△AOM∽△ADC，
∴OM：CD=AM：AC，
即r：1=（4-r）：4，
解得r=．
故选A．
点评：此题考查直角三角形中内切圆的性质及利用相似三角形求内切圆的半径．
分析：设圆O与AC的切点为M，圆的半径为r，求得△AOM∽△ADC，利用相似比作为相等关系可列式：1=（4-r）：4，解之即可．
解答：
解：设圆O与AC的切点为M，圆的半径为r，如图，连接OM，
∵∠C=90°
∴CM=r，
∵△AOM∽△ADC，
∴OM：CD=AM：AC，
即r：1=（4-r）：4，
解得r=
．故选A．
点评：此题考查直角三角形中内切圆的性质及利用相似三角形求内切圆的半径．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
24、如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点G．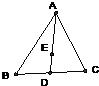
14、如图，E为△ABC的重心，ED=3，则AD=
（2012•井研县模拟）如图，D为△ABC的AB边上的一点，∠ABC=∠ACD，AD=2cm，AB=3cm，则AC=（ ）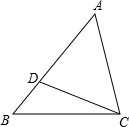
如图，D为△ABC的边AB上一点，且∠ABC=∠ACD，AD=3cm，AB=4cm，则AC的长为（ ）
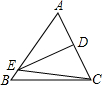如图，DE为△ABC中AC边的中垂线，BC=8，AB=10，则△EBC的周长是（ ）