题目内容
【题目】若一次函数y=kx+4的图象经过点(1,2)
(1)求k的值;
(2)在所给直角坐标系中画出此函数的图象;
(3)根据图象回答:当x 时,y>0
【答案】（1）y=2x+4；（2）见解析；（3）x<2.
【解析】
（1）根据点的坐标利用待定系数法即可求出函数表达式；
（2）令y=0求出x值，根据一次函数图象与坐标轴的交点坐标即可画出函数图象；
（3）寻找到函数图象在x轴上方时x的取值范围，此题得解．
（1）将(1,2)和(0,4)分别代入y=kx+b,
得：
,解得：
，
∴一次函数的表达式为y=2x+4.
（2）∵当y=2x+4=0时，x=2.
当x=0时，y=0+4=4.
∴函数图象过点(0,4)和(2,0).
画出函数图象如图所示：
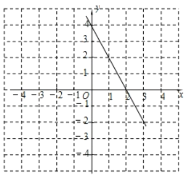
（3）观察函数图象发现：当x<2时，函数图象在x轴上方
故答案为：x<2.
轻松课堂单元期中期末专题冲刺100分系列答案
【题目】为了迎接元旦，孝昌县政府要在广场上设计一座三角形展台，要求园林工人把它的每条边上摆放上相等盆数的盆栽鲜花（如图所示的每个小圆圈表示一盆鲜花）以美化环境，如果每条边上摆放两盆鲜花，共需要3盆鲜花；如果每条边上摆放3盆鲜花，共需要6盆鲜花；…，按此要求摆放下去：
（1）根据图示填写下表：
每条边上摆放的盆数（ | 2 | 3 | 4 | 5 | 6 | … |
共需要的盆数（ | 3 | 6 | … |
（2）如果要在每条边上摆放
盆鲜花，那么需要鲜花的总盆数 ．
（3）请你帮园林工人参考一下，能否用2020盆鲜花作出符合要求的摆放？如果能，请计算出每条边上应摆放花的盆数；如果不能，请说明理由．
【题目】陆老师去水果批发市场采购苹果，他看中了A，B两家苹果，这两家苹果品质一样，零售价都我6元/千克，批发价各不相同．
A家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠．
B家的规定如下表：
数量范围（千克） | 0～500部分 | 500以上～1500 | 1500以上～2500部分 | 2500以上部分 |
价格补贴 | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
（1）如果他批发700千克苹果，则他在A、B两家批发分别需要多少元？
（2）如果他批发x千克苹果（1500＜x＜2000），请你分别用含x的代数式表示他在A、B两家批发所需的费用；
（3）A、B两店在互相竞争中开始了互怼，B说A店的苹果总价有不合理的，有时候买的少反而贵，忽悠消费者；A说B的总价计算太麻烦，把消费者都弄糊涂了；旁边陆老师听完，提出两个问题希望同学们帮忙解决：
问题1：能否举例说明A店买的多反而便宜?
问题2：B店老板比较聪明，在平时工作中发现有巧妙的方法：总价=购买数量×单价+价格补贴；
注:不同的单价，补贴价格也不同；只需提前算好即可填下表：
数量范围（千克） | 0～500部分 | 500以上～1500 | 1500以上～2500 | 2500以上部分 |
价格补贴 | 0元 | 300 |
