题目内容
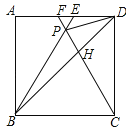
【题目】如图 1，在等边△ABC 中，AD是∠BAC的平分线，一个含有120°角的△MPN的顶点P（∠MPN=120°）与点D重合，一边与AB垂直于点E，另一边与AC交于点F．
①请猜想并写出AE+AF与AD之间满足的数量关系，不必证明．
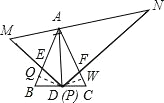
②在图1的基础上，若△MPN绕着它的顶点P旋转，E、F仍然是△MPN的两边与AB、AC的交点，当三角形纸板的边不与AB垂直时，如图2，（1）中猜想是否仍然成立？说明理由．
③如图 3，若△MPN绕着它的顶点P旋转，当△MPN的一边与AB的延长线相交，另一边与AC的反向延长线相交时，AE、AF与AD之间又满足怎样的数量关系？直接写出结论，不必证明．
【答案】（1）AE+AF=
AD，（2）仍然成立，（3）AE﹣AF=AD．
【解析】
（1）根据题意利用等边三角形、角平分线直角三角形、锐角三角函数推理可得出
（2）根据（1）中结论，利用图1，可推理得出结论仍然成立；
（3）结合（1）（2）可推理出
解：（1）
(2)
仍然成立，
证明：过 D 点作 AB、AC 的垂线，垂足为 Q、W，
可证△DEQ≌△DFW，
∴AQ=AW，EQ=FW，
∴仍然满足
练习册系列答案
相关题目
