题目内容
【题目】已知:如图, AD=CD=CB=AB=a,DA∥CB,AB⊥CB,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.
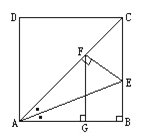
(1)求AC的长;(2)求证:AB=![]() AG.
AG.
【答案】(1)、![]() a;(2)、证明过程见解析.
a;(2)、证明过程见解析.
【解析】
试题分析:(1)、首先根据∠B=90°,AB=BC得出△ABC为等腰直角三角形,然后根据勾股定理求出AC的长度;(2)、根据角平分线的性质得出AF=AB=a,根据等腰直角△AFG的性质求出AG的长度,得出答案.
试题解析:(1)、∵AB⊥BC ∴∠B=90° ∵AB=BC=a ∴△ABC为等腰直角三角形
∴AC=![]() =
=![]() a
a
、∵△ABC为等腰直角三角形 ∴∠CAB=45° ∵FG⊥AB ∴△AFG为等腰直角三角形
∵AE平分∠CAB EF⊥AC EB⊥AB ∴△AEF≌△AEB ∴AF=AB=a
∴根据等腰直角△AFG的勾股定理可得:AG=![]() a ∴AB=
a ∴AB=![]() AG.
AG.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目