题目内容
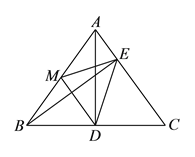
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB的值为多少时,四边形MENF是正方形(只写结论,不需证明).

【答案】(1)证明见解析(2)四边形MENF是菱形(3)2:1
【解析】试题分析:(1)求出AB=DC,∠A=∠D=90°,AM=DM,根据全等三角形的判定定理推出即可;
(2)根据三角形中位线定理求出NE∥MF,NE=MF,得出平行四边形,求出BM=CM,推出ME=MF,根据菱形的判定推出即可;
(3)求出∠EMF=90°,根据正方形的判定推出即可.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴A=∠D=90°,AB=DC,
∴M是AD的中点,
∴AM=DM,
在△ABM和△DCM中,  ,
,
∴△ABM≌△DCM(SAS),
(2)四边形MENF是菱形;理由如下:
∴E、N、F分别是线段BM、BC、CM的中点,
∴EN是△BCM的中位线,
∴EN=![]() CM=FM,EN∥FM,
CM=FM,EN∥FM,
∴四边形MENF是平行四边形,
同理:NF是△BCM的中位线,
∴NF=![]() BM,
BM,
∴BM=CM,
∴EN=NF,
∴四边形MENF是菱形;
(3)当AD:AB=2:1时,四边形MENF是正方形;理由如下:
∴AD:AB=2:1,M是AD的中点,
∴AB=AM,
∴△ABM是等腰直角三角形,
∴∠AMB=45°,
同理:DMC=45°,∠EMF=180°﹣45°﹣45°=90°,
由(2)得:四边形MENF是菱形,
∴四边形MENF是正方形;
故答案为:2:1.

练习册系列答案
相关题目