题目内容
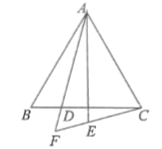
【题目】在等边![]() 中,点
中,点![]() 是边
是边![]() 上一点.作射线
上一点.作射线![]() ,点
,点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() .连接
.连接![]() 并延长,交射线
并延长,交射线![]() 于点
于点![]() .
.
(1)如图,连接![]() ,
,
①![]() 与
与![]() 的数量关系是__________;
的数量关系是__________;
②设![]() ,用
,用![]() 表示
表示![]() 的大小;
的大小;
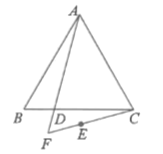
(2)如图,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1) ①AB=AE;②∠BCF=![]() ;(2) AF-EF=CF,理由见详解.
;(2) AF-EF=CF,理由见详解.
【解析】
(1)①根据轴对称性,即可得到答案;
②由轴对称性,得:AE=AB,∠BAF=∠EAF=![]() ,由
,由![]() 是等边三角形,得AB=AC,∠BAC=∠ACB=60°,再根据等腰三角形的性质和三角形内角和等于180°,即可求解;
是等边三角形,得AB=AC,∠BAC=∠ACB=60°,再根据等腰三角形的性质和三角形内角和等于180°,即可求解;
(2)作∠FCG=60°交AD于点G,连接BF,易证FCG是等边三角形,得GF=FC,再证ACGBCF(SAS),从而得AG=BF,进而可得到结论.
(1)①∵点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() ,
,
∴AB和AE关于射线![]() 的对称,
的对称,
∴AB=AE.
故答案是:AB=AE;
②∵点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() ,
,
∴AE=AB,∠BAF=∠EAF=![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°,
∴∠EAC=60°-2![]() ,AE=AC,
,AE=AC,
∴∠ACE=![]() ,
,
∴∠BCF=∠ACE-∠ACB=![]() -60°=
-60°=![]() .
.
(2)AF-EF=CF,理由如下:
作∠FCG=60°交AD于点G,连接BF,
∵∠BAF=∠BCF=![]() ,∠ADB=∠CDF,
,∠ADB=∠CDF,
∴∠ABC=∠AFC=60°,
∴FCG是等边三角形,
∴GF=FC,
∵![]() 是等边三角形,
是等边三角形,
∴BC=AC,∠ACB=60°,
∴∠ACG=∠BCF=![]() .
.
在ACG和BCF中,
∵ ,
,
∴ACGBCF(SAS),
∴AG=BF,
∵点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() ,
,
∴AG=BF=EF,
∵AF-AG=GF,
∴AF-EF=CF.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】对于代数式,不同的表达形式能表现出它的不同性质.例如代数式![]() ,若将其写成
,若将其写成![]() 的形式,就能看出不论字母x取何值,它都表示正数;若将它写成
的形式,就能看出不论字母x取何值,它都表示正数;若将它写成![]() 的形式,就能与代数式B=
的形式,就能与代数式B=![]() 建立联系.下面我们改变x的值,研究一下A,B两个代数式取值的规律:
建立联系.下面我们改变x的值,研究一下A,B两个代数式取值的规律:
x | -2 | -1 | 0 | 1 | 2 | 3 |
| 10 | 5 | 2 | 1 | 5 | |
| 17 | 10 | 5 |
(1)完成上表;
(2)观察表格可以发现:
若x=m时,![]() ,则x=m+1时,
,则x=m+1时,![]() .我们把这种现象称为代数式A参照代数式B取值延后,此时延后值为1.
.我们把这种现象称为代数式A参照代数式B取值延后,此时延后值为1.
①若代数式D参照代数式B取值延后,相应的延后值为2,求代数式D;
②已知代数式![]() 参照代数式
参照代数式![]() 取值延后,请直接写出b-c的值:________.
取值延后,请直接写出b-c的值:________.
【题目】一分钟投篮测试规定:满分为![]() 分,成绩达到
分,成绩达到![]() 分及以上为合格,成绩达到
分及以上为合格,成绩达到![]() 分及以上为优秀.甲、乙两组各
分及以上为优秀.甲、乙两组各![]() 名学生的某次测试成绩如下:
名学生的某次测试成绩如下:
成绩(分) |
|
|
|
|
|
|
|
|
|
|
甲组(人) |
|
|
|
|
|
|
|
|
|
|
乙组(人) |
|
|
|
|
|
|
|
|
|
|
![]() 请补充完成下面的成绩分析表:
请补充完成下面的成绩分析表:
统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
甲组 |
|
|
|
| ________ |
乙组 | ________ |
| ________ |
|
|
![]() 你认为甲、乙两组哪一组的投篮成绩较好?请写出两条支持你的观点的理由.
你认为甲、乙两组哪一组的投篮成绩较好?请写出两条支持你的观点的理由.