题目内容
【题目】提出问题：“周长一定的长方形，当邻边长度满足什么条件时面积最大？”
探究发现：如图所示，小敏用4个完全相同的、邻边长度分别为a、b的长方形拼成一个边长为（a+b）的正方形（其中a、b的和不变，但a、b的数值及两者的大小关系都可以变化）．仔细观察拼图，我们发现，如果右图中间有空白图形F，那么它一定是正方形
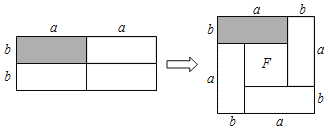
（1）空白图形F的边长为 ；
（2）通过计算左右两个图形的面积，我们发现（a+b）2、（a﹣b）2和ab之间存在一个等量关系式．
①这个关系式是 ；
②已知数x、y满足：x+y＝6，xy＝
，则x﹣y＝ ；
问题解决：
问题：“周长一定的长方形，当邻边长度满足什么条件时面积最大？”
①对于周长一定的长方形，设周长是20，则长a和宽b的和是 面积S＝ab的最大值为 ，此时a、b的关系是 ；
②对于周长为L的长方形，面积的最大值为 ．
活动经验：
周长一定的长方形，当邻边长度a、b满足 时面积最大．
【答案】探究发现：（1）a﹣b；（2）①（a+b）2﹣（a﹣b）2＝4ab；②5或﹣5；问题解决：①10，25，a＝b；②
L2；活动经验：a＝b．
【解析】
探究发现
（1）由图可知：空白图形F的边长为：a-b；
（2）①由矩形的性质得出左图形的面积为：2a×2b=4ab，由正方形的性质得出右图形的面积为：（a+b）2-（a-b）2，即可得出答案；
②由①得出（x-y）2=25，即可得出答案；
问题解决
①由长方形的性质得出a+b=10，面积S=ab=a（10-a）=-a2+10a=-（a-5）2+25，由二次函数的性质即可得出答案；
②由长方形的性质得出面积
；由二次函数的性质即可得出答案；
活动经验
根据前面的问题即可得出结论．
（1）由图可知：空白图形F的边长为：a﹣b，
故答案为：a﹣b；
（2）①左图形的面积为：2a×2b＝4ab，
右图形的面积为：（a+b）2﹣（a﹣b）2，
∴（a+b）2﹣（a﹣b）2＝4ab，
故答案为：（a+b）2﹣（a﹣b）2＝4ab；
②由（a+b）2﹣（a﹣b）2＝4ab得：（x+y）2﹣（x﹣y）2＝4xy，
即：62﹣（x﹣y）2＝4×
，
∴（x﹣y）2＝25，
∴x﹣y＝5或x﹣y＝﹣5，
故答案为：5或﹣5；
问题解决：
解：①∵长方形的周长是20，
∴2（a+b）＝20，
∴a+b＝10，则b＝10﹣a，
∴面积S＝ab＝a（10﹣a）＝﹣a2+10a＝﹣（a﹣5）2+25，
∴a＝5时，S＝ab的最大值为25，
此时a、b的关系是a＝b，
故答案为：10，25，a＝b；
②对于周长为L的长方形，
设一边长为a，则邻边长为
﹣a，
∴面积；
∴面积的最大值为L2；
故答案为：L2；
活动经验：
解：周长一定的长方形，当邻边长度a、b满足a＝b时面积最大；
故答案为：a＝b．
