题目内容
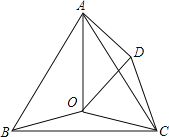
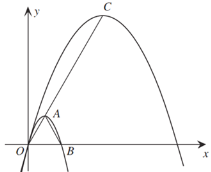
【题目】如图,在 △ABC和 △ADE中,∠BAD=∠CAE, ∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线);
(2)请证明你写出的两对相似三角形.

【答案】(1)见解析;(2)见解析.
【解析】
(1)△ABC∽△ADE,△ABD∽△ACE;
(2)∠BAD=∠CAE,在此等式两边各加∠DAC,可证∠BAC=∠DAE,再结合已知中的∠ABC=∠ADE,可证△ABC∽△ADE;利用△ABC∽△ADE,可得AB:AD=AC:AE,再结合∠BAD=∠CAE,也可证△BAD∽△CAE.
(1)△ABC∽△ADE,△ABD∽△ACE;
(2)①证△ABC∽△ADE,
∵∠BAD=∠CAE,
∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
又∵∠ABC=∠ADE,
∴△ABC∽△ADE.
②证△ABD∽△ACE,
∵△ABC∽△ADE,
∴![]() .
.
又∵∠BAD=∠CAE,
∴△ABD∽△ACE.

【题目】(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
球的类别 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?