题目内容
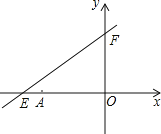
【题目】如图,直线y=kx+6与x轴y轴分别交于点E,F.点E的坐标为(-8,0),点A的坐标为(-6,0).
(1)求K的值;
(2)若点P(x,y)是第二象限内该直线上的一个动点,当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.
【答案】(1)k=![]() ;(2)
;(2)![]() x+18 (-8<x<0);(3)
x+18 (-8<x<0);(3)![]() .
.
【解析】(1)把E(-8,0)代入直线y=kx+6即可求出k=![]() ,
,
(2)根据点A的坐标为(-6,0),求出OA,根据点P(x,y)是第二象限内的直线上的一个动点,得出△OPA的高是点P的纵坐标,得出面积S=![]() ×6×(
×6×(![]() x+6),
x+6),
(3)当点P在直线y=kx+6上,且在x轴上方时,S=![]() x+18=
x+18=![]() ,当点P在直线y=kx+6上,且在x轴下方时,S=
,当点P在直线y=kx+6上,且在x轴下方时,S=![]() x-18=
x-18=![]() ,分别求出x的值,得出点P的坐标即可.
,分别求出x的值,得出点P的坐标即可.
解:(1)∵直线y=kx+6过点E(-8,0),∴0=-8k+6,
k=![]() ,
,
(2)∵点A的坐标为(-6,0),∴OA=6,
∵点P(x,y)是第二象限内的直线上的一个动点,
∴△OPA的面积S=![]() ×6×(
×6×(![]() x+6)=
x+6)=![]() x+18 (-8<x<0),
x+18 (-8<x<0),
(3)设点P(m,n)时,其面积S=![]() ,
,
则![]() ,解得
,解得![]() ,
,
则![]() 或者
或者![]() (舍去),
(舍去),
![]() 时,
时,![]() ,解得
,解得![]() ,
,
故P(![]() ,
,![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.
“点睛”此题考查了一次函数综合,用到的知识点是一次函数的图象和性质、求函数解析式,关键是根据题意列出算式,注意分两种情况分析.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
