题目内容
(1)式子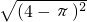 +|π-6|与
+|π-6|与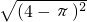 -|π-6|的值与π有否关系?请说明理由;当x取不同的值时,代数式
-|π-6|的值与π有否关系?请说明理由;当x取不同的值时,代数式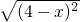 -|x-6|的值会发生什么变化?
-|x-6|的值会发生什么变化?
(2)设m>0,a≠b,易知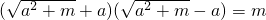 ,如果还有
,如果还有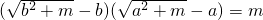 ,问a、b之间应满足什么关系?指出结论,再说明理由.
,问a、b之间应满足什么关系?指出结论,再说明理由.
解:(1)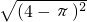 +|π-6|与π有关系,
+|π-6|与π有关系,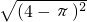 -|π-6|与π无关系.
-|π-6|与π无关系.
∵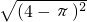 +|π-6|=4-π+(6-π)=10-2π,
+|π-6|=4-π+(6-π)=10-2π,
∴与π有关;
∵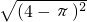 -|π-6|=4-π-(6-π)=-2
-|π-6|=4-π-(6-π)=-2
∴与π无关;
∵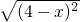 -|x-6|=|x-4|-|x-6|
-|x-6|=|x-4|-|x-6|
当x<4时,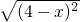 -|x-6|=4-x-(6-x)=-2;
-|x-6|=4-x-(6-x)=-2;
当4≤x<6时,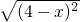 -|x-6|=x-4-(6-x)=2x-10;
-|x-6|=x-4-(6-x)=2x-10;
当x≥6时,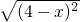 -|x-6|=x-4-(x-6)=2.
-|x-6|=x-4-(x-6)=2.
(2)a+b=0.理由如下:
∵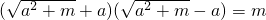 和
和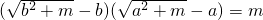 ,
,
∴ ,
,
∴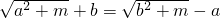 ,
,
两边平方,整理得, ,
,
再平方化简得a2=b2,
即a2-b2=0?(a+b)(a-b)=0,
∵a-b≠0,
∴a+b=0.
分析:(1)利用 =|a|与绝对值的含义把式子
=|a|与绝对值的含义把式子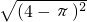 +|π-6|与
+|π-6|与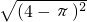 -|π-6|进行化简即可得到与π的关系;先由
-|π-6|进行化简即可得到与π的关系;先由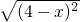 -|x-6|=|x-4|-|x-6|,然后分区间讨论:当x<4或4≤x<6或x≥6,分别去绝对值即可;
-|x-6|=|x-4|-|x-6|,然后分区间讨论:当x<4或4≤x<6或x≥6,分别去绝对值即可;
(2)根据条件易得 ,移项得到
,移项得到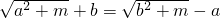 ,然后两边平方最后可得a2=b2,而a≠b,即可a=-b.
,然后两边平方最后可得a2=b2,而a≠b,即可a=-b.
点评:本题考查了考查了二次根式的化简求值: =|a|.也考查了绝对值的含义以及代数式的变形能力.
=|a|.也考查了绝对值的含义以及代数式的变形能力.
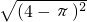 +|π-6|与π有关系,
+|π-6|与π有关系,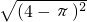 -|π-6|与π无关系.
-|π-6|与π无关系.∵
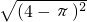 +|π-6|=4-π+(6-π)=10-2π,
+|π-6|=4-π+(6-π)=10-2π,∴与π有关;
∵
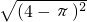 -|π-6|=4-π-(6-π)=-2
-|π-6|=4-π-(6-π)=-2∴与π无关;
∵
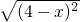 -|x-6|=|x-4|-|x-6|
-|x-6|=|x-4|-|x-6|当x<4时,
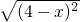 -|x-6|=4-x-(6-x)=-2;
-|x-6|=4-x-(6-x)=-2;当4≤x<6时,
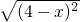 -|x-6|=x-4-(6-x)=2x-10;
-|x-6|=x-4-(6-x)=2x-10;当x≥6时,
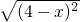 -|x-6|=x-4-(x-6)=2.
-|x-6|=x-4-(x-6)=2.(2)a+b=0.理由如下:
∵
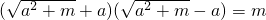 和
和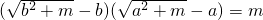 ,
,∴
 ,
,∴
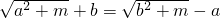 ,
,两边平方,整理得,
 ,
,再平方化简得a2=b2,
即a2-b2=0?(a+b)(a-b)=0,
∵a-b≠0,
∴a+b=0.
分析:(1)利用
 =|a|与绝对值的含义把式子
=|a|与绝对值的含义把式子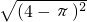 +|π-6|与
+|π-6|与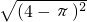 -|π-6|进行化简即可得到与π的关系;先由
-|π-6|进行化简即可得到与π的关系;先由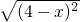 -|x-6|=|x-4|-|x-6|,然后分区间讨论:当x<4或4≤x<6或x≥6,分别去绝对值即可;
-|x-6|=|x-4|-|x-6|,然后分区间讨论:当x<4或4≤x<6或x≥6,分别去绝对值即可;(2)根据条件易得
 ,移项得到
,移项得到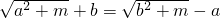 ,然后两边平方最后可得a2=b2,而a≠b,即可a=-b.
,然后两边平方最后可得a2=b2,而a≠b,即可a=-b.点评:本题考查了考查了二次根式的化简求值:
 =|a|.也考查了绝对值的含义以及代数式的变形能力.
=|a|.也考查了绝对值的含义以及代数式的变形能力. 
练习册系列答案
相关题目
下列式子中,正确的是( )
A、
| |||
B、-
| |||
C、
| |||
D、
|
已知:
=
,那么下列式子成立的是( )
| 3 |
| x |
| 2 |
| y |
| A、3x=2y | ||||
| B、xy=6 | ||||
C、
| ||||
D、
|
如果A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=
(k<0)图象上的三个点,且x1<x2<0<x3,那么,下列式子成立的是( )
| k |
| x |
| A、y2<y1<y3 |
| B、y1<y2<y3 |
| C、y3<y1<y2 |
| D、y3<y2<y1 |